Контрольная работа: Линейный множественный регрессивный анализ

Таким образом, смертность населения по причине болезни органов кровообращения на 100000 населения увеличивается примерно на 0,12 % при увеличении потребления мяса и мясопродуктов на душу населения на 1 %, на 0,21% при увеличении на 1% потребления сахара на душу населения и на 0,37% при увеличении потребления хлебных продуктов на душу населения на 1%.

А при увеличении оценки ВВП по паритету покупательной способности в 1994 г. на душу населения на 1% результативный показатель, наоборот, уменьшится на 0,59%. Увеличение же потребления фруктов и ягод на душу населения на 1% повлечет снижение смертности примерно на 1,02%.

3. Оценим статистическую значимость параметров регрессионной модели с помощью t -критерия.

Расчетные значения критерия для пяти заданных параметров получили с помощью инструмента «Регрессия» надстройки «Анализ данных» приложения MS Excel (результаты вычисления – в Приложении 7):

Поскольку , то коэффициенты b₁ , b₂ , b₃ , b₄ , b₅ не являются значимыми для построенной модели.

Адекватность модели проверим с помощью F -критерия.

Величина множественного коэффициента детерминации R² =0,799, также рассчитана с помощью инструмента «Регрессия» надстройки «Анализ данных» приложения MS Excel (результаты вычисления – в Приложении 7). Построенную модель на основе этого параметра можно признать достаточно качественной. А изменение результативного показателя примерно на 80 % обусловлено влиянием факторов, включенных в модель.

Наблюдаемое значение F–критерия превышает табличное: 16,65 > 4,52, т.е. выполнено неравенство , а значит, в 95 % случаев уравнение регрессии статистически значимо и отражает существенную зависимость между факторами и результативным показателем.

Уравнение можно признать надежным и значимым, доказывающим наличие исследуемой зависимости.

4. Оценим качество построенного уравнения с помощью средней ошибки аппроксимации.

Проведем необходимые дополнительные расчеты с вспомогательной таблицей (графа 11 Приложения 6). На основе полученных данных найдем значение средней ошибки аппроксимации:

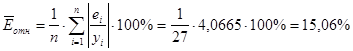
Полученное значение средней ошибки аппроксимации подтверждает удовлетворительную точность построенной модели.

5. Используя метод многошагового регрессионного анализа, построим регрессионную модель только со значимыми факторами и оценим ее параметры.

Поскольку модель со всеми заданными факторами уже построена, и значимость каждого фактора рассчитана, можем перейти к следующему шагу анализа, исключив из модели самый незначимый фактор.

Исключаем фактор Х₆ - оценка ВВП по паритету покупательной способности в 1994 г. на душу населения (в % к США). Строим новую модель с оставшимися факторами:

Параметры данного уравнения найдем с помощью инструмента «Регрессия» надстройки «Анализ данных» приложения MS Excel (результаты вычисления – в Приложении 8):

b₀ =11,3789103724081

b₁ = -0,140477614195711