Контрольная работа: Математические модели в экономике

Графическое представление результатов сглажевания

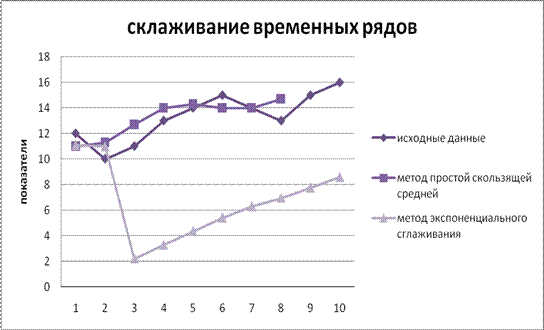
Ниже в таблице приведены исходный ряд данных yt и сглаженные двумя способами уровни исходного ряда. При этом при сглаживании при помощи метода простой скользящей средней использовался интервал сглаживания m = 3.

При сглаживании экспоненциальным методом был доведён параметр сглаживания а = 0,1

Соответственно, числовая последовательность весов имела вид:

t	yt	методом простой скользящей средней	_методом y экспоненциального сглаживания
1	12	-	11.1
2	10	11	10.99
3	11	11.3	2.2
4	13	12.7	3.28
5	14	14	4.35
6	15	14.3	5.42
7	14	14	6.29
8	13	14	6.96
9	15	14.7	7.76
10	16	-	8.58

Чтобы правильно подобрать лучшую кривую роста для моделирования и прогнозирования экономического явления, необходимо знать особенности каждого вида кривых в экономике часто используется полиномиальная кривая роста, как кривая с полиномом первой степени.

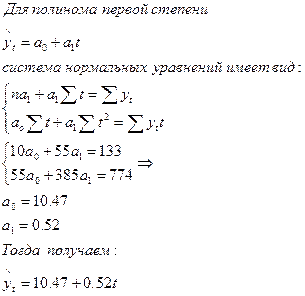
Параметр a1 называют линейным приростом. Для полинома первой степени характерен постоянный закон роста. Если посчитать первые приросты по формуле

ut = yt – yt -1, t = 2,3,…,n,

то они будут постоянной величиной и равны а 1.

Значения прироста для полиномов любого порядка не зависят от значений самой функции .

Полиномные кривые роста можно использовать для аппроксимации (приближения) и прогнозирования экономических процессов, в которых последующее развитие не зависит от достигнутого уровня. Исходный временной ряд предварительно сглаживается методом простой скользящей средней.

Необходимо оценить адекватность и точность построения модели, т.е. необходимо выполнение следующих условий:

a) проверка случайности колебаний уровней остаточной последовательности:

Проверку случайности уровней ряда проведем по критерию пиков, должно выполняться:

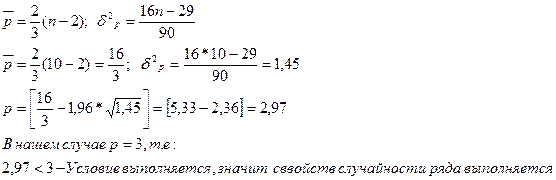
t	Фактическое	Расчётное	Отклонение	Точки пиков
1 2 3 4 5 6 « 1 2 3 4 5 6 7 8 9 » К-во Просмотров: 546 Бесплатно скачать Контрольная работа: Математические модели в экономике >>> Скачать <<< Меню Поиск