Контрольная работа: Метод Лобачевського-Греффе

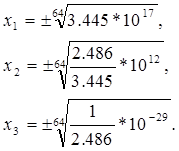
Логарифмуючи, отримаємо:

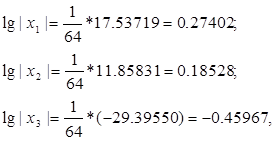
а, отже,

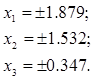
Для визначення знаків коренів зауважимо, що згідно з правилом Декарта наше рівняння має один негативний корінь та два позитивних корені, причому

Тому найбільшим за модулем має бути негативний корінь, і ми остаточно маємо:

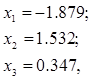
причому співвідношення виконано в межах заданої точності. Для порівняння можна взяти точні значення коренів, отримані за формулою Кардана:

x1=2cos160°=-1.87938;

x2=2cos40°=-1.53208;

x3=2cos80°=0.34730.

Зауважимо, що в нашому випадку обчислення коренів настільки спростилося завдяки тому, що крайні коефіцієнти рівняння дорівнюють 1. Взагалі, при використанні метода Лобачевского-Греффе радимо попередньо перетворити рівняння так, щоб старший коефіцієнт рівняння дорівнював 1, а вільний член рівняння дорівнював ±1.

Програма обчислення коренів рівняння наведена в ДодаткуA.

Висновки

В роботі ми розглянули метод Лобачевского-Греффе, навчилися використовувати його для розв’язання алгебраїчних рівнянь.

Вивчивши алгоритм методу, склали програму мовою C++, що спрощує його обчислення. Вона докладно описується в додаткуA.

Перелік посилань

1. „Основы вычислительной математики”; Б. П. Демидович, І. А. Марон; „Государственное издательство физико-математической литературы”, Москва, 1960

2. „Математический анализ”; А. Я. Дороговцев; „Либідь”, Київ, 1993

3. „Программирование на языке C++”; С. А. Калоєров; „Юго-восток”, Донецьк, 2004

Додаток A

Скласти програму для обчислення коренів алгебраїчного рівняння

Код програми, що обчислює корені алгебраїчного рівняння методом Лобачевского-Греффе.

#include<iostream.h>

#include<math.h>

void main()

{int j,s,k,i,n,step,izo;

double summ,akms,akps,b;

cout<<"Введите степень уравненийа\n";

cin>>step;