Контрольная работа: Основы математического анализа

1. Множества и операции над множествами

Напомним основные обозначения, понятия, относящиеся к множествам, которых будем придерживаться дальше.

Начнем с основного понятия, которое встречается практически в каждом разделе математики - это понятие множества.

Множество - это совокупность, набор элементов, объединенных общими свойствами.

Множества обозначаются заглавными латинскими буквами , а элементы множества строчными латинскими буквами .

Запись означает, что есть множество с элементами , которые связаны между собой какой-то функцией .

Замечание. Элементы в множество входят по одному разу, т.е. без повторений.

Основные операции:

1. Принадлежность элемента множеству:

где -- элемент и -- множество (элемент принадлежит множеству ).

2. Непринадлежность элемента множеству:

где -- элемент и -- множество (элемент не принадлежит множеству ).

3. Объединение множеств: .

Объединением двух множестви называется множество , которое состоит из элементов множеств и , т.е.

или

4. Пересечение множеств: .

Пересечением двух множестви называется множество , которое состоит из общих элементов множеств и , т.е.

и

5. Разность множеств: .

Разностью двух множестви , например, множество минус множество , называется множество , которое состоит из элементов множества , которых нет в множестве , т.е.

и

6. Симметрическая разность множеств:

.

Симметрической разностью двух множестви называется множество , которое состоит из не общих элементов множеств и , т.е.

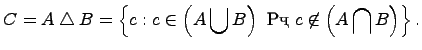
7. Дополнение множества: .

Если предположим, что множество является подмножеством некоторого универсального множества , тогда определяется операция дополнения:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--