Контрольная работа: Основы математического анализа

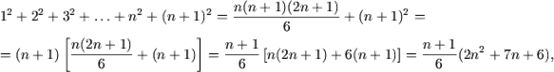
и, так как 2n² + 7n + 6 = (2n + 3)(n + 2), получим

и, следовательно, исходное равенство справедливо для любого натурального n.

d) При n = 1 равенство справедливо: 1=1. Допустим, что имеет место

и докажем, что

Действительно,

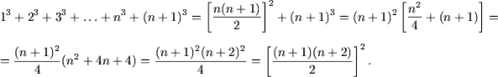
e) Утверждение P(1) справедливо: 2=2. Допустим, что равенство

справедливо, и докажем, что оно влечет равенство

Действительно,

Следовательно, исходное равенство имеет место для любого натурального n.

f) P(1) справедливо: ¹ /₃ = ¹ /₃ . Пусть имеет место равенство P(n):

.

Покажем, что последнее равенство влечет следующее:

Действительно, учитывая, что P(n) имеет место, получим

Таким образом, равенство доказано.

g) При n = 1 имеем a + b = b + a и, следовательно, равенство справедливо.

Пусть формула бинома Ньютона справедлива при n = k, то есть,

Тогда