Контрольная работа: Особливі точки рівняння

Якщо розв’язки комплексні з дійсною частиною , відмінною від нуля, то особлива точка - фокус (рис.1, в), причому стійкий , якщо й нестійкий , якщо . На рис.1в стрілками показаний напрямок руху при зростанні у випадку стійкого фокуса.

Зауваження. У випадку фокуса траєкторії можуть бути закручені навколо (0,0) у різних напрямках. Для того, щоб визначити напрямок закручування, досить обчислити вектор швидкості в якій-небудь точці, наприклад, в (0,1). Аналогічно досліджується напрямок руху у випадку центра й виродженого вузла.

Якщо розв’язки комплексні чисто мнимі (), то особлива точка - центр (рис.1, г). Центр є стійкою, але не асимптотично стійкою точкою спокою.

Якщо розв’язки рівні й ненульові (тобто ), то особлива точка може бути виродженим вузлом (рис.1, д) або дикритичним вузлом (рис.1, е), причому дикритичний вузол має місце тільки у випадку системи (або рівняння ), а у всіх інших випадках при особлива точка є виродженим вузлом. У випадку виродженого вузла всі траєкторії дотикаються однієї прямої, спрямованої вздовж єдиного власного вектора, що відповідає . Дикритичний вузол може бути стійким і нестійким .

Якщо ж один або обидва розв’язки рівняння (5) дорівнюють нулю, то , і, отже, дріб у правій частині рівняння (4) скорочується. Рівняння набуває вигляду , і розв’язок на площині XOY зображуються паралельними прямими.

2. Задача 1

Дослідити особливі точки рівняння. Накреслити інтегральні криві на площині XOY:

Розв’язання.

Для дослідження особливої точки рівняння

треба знайти розв’язок характеристичного рівняння

У нас , , , . Складаємо характеристичне рівняння

і розв’язуємо його відносно

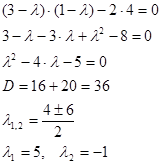
Розв’язки характеристичного рівняння дійсні й мають різні знаки.

Отже, особлива точка (0,0) - сідло. Сідло є нестійкою точкою спокою.

1. Перший спосіб побудови інтегральних кривих.

Власний вектор , що відповідає власному числу , знаходимо, підставляючи в рівняння

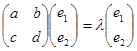
значення . Маємо

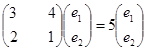
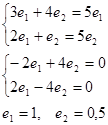
Власний вектор (1; 1/2) матриці коефіцієнтів даної системи, відповідає власному числу .

Далі, власний вектор , що відповідає власному числу , знаходимо, підставляючи в рівняння

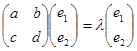
значення . Маємо