Контрольная работа: Особливі точки рівняння

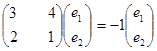
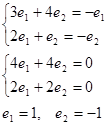
Власний вектор (1; - 1) матриці коефіцієнтів даної системи, відповідає власному числу .

На площині будуємо прямі, спрямовані вздовж власних векторів (1; 1/2) і (1; - 1), а потім будуємо гіперболи.

2. Другий спосіб побудови інтегральних кривих.

Знайдемо сепаратриси сідла, тобто прямі, що розділяють гіперболи різних типів, які є фазовими кривими системи (тобто асимптоти цих гіпербол).

Прямі, що проходять через особливу точку (0,0), шукаємо у вигляді . Підставляючи у вихідне рівняння

,

одержуємо рівняння для визначення коефіцієнта

Таким чином, маємо дві шукані прямі

,.

3. Напрямок руху по траєкторіях. Для з'ясування напрямку руху по траєкторіях досить побудувати в якій-небудь точці вектор швидкості . Наприклад, у точках та вектор швидкості дорівнює

, ,

у точках та вектор швидкості дорівнює

, ,

у точках та вектор швидкості дорівнює

, ,

у точках та вектор швидкості дорівнює

, .

Приблизний вид сім’ї інтегральних кривих зображено на рисунку 2.

Рис.2. Положення рівноваги й інтегральні криві [6]

3. Задача 2

Дослідити особливі точки рівняння. Накреслити інтегральні криві на площині XOY: