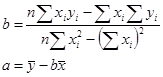Контрольная работа: Побудова лінійної регресійної моделі
Дані, що не є тимчасовими, прийнято називати просторовими. Звичайно вони збираються з рознесених просторово точок і є крапками вибірки обсягу п і розмірності до к = т + 1 (число к на 1 більше числа факторів т ). Вимоги репрезентативності вибірки припускають випадковість добору і достатній обсяг вибірки з виконанням умови п >> к . Це завжди варто пам'ятати при побудові моделей, І інакше можливе одержання зміщених оцінок. Про середній курс долара в місті, наприклад, не можна судити по обмінних пунктах у районі міського вокзалу. Прикладами просторових даних є дані по виробництву, продажу, споживанню, цінам у різних точках міста (країни) у визначений момент часу. На макроекономічному рівні це можуть бути дані по розподілі трудових і матеріальних ресурсів по регіонах країни.
2. Метод найменших квадратів
Модель парної лінійної регресії є власне кажучи лінійною апроксимацією (наближенням) реальної лінії регресії у(х) як умовного математичного чекання випадкового показника Y. Специфікація моделі може бути записана як:![]()
![]()
Тут передбачається, що α і β - точні значення параметрів моделі; хі - відомі вибіркові значення фактора; εі - випадкові помилки моделі в і-й точці з імовірностними властивостями генеральної сукупності. Очевидно, випадкові значення показника yі при цих умовах мають той же розподіл, що і помилки εі (зі зсувом ![]() ). Для спрощення запису ми позначаємо параметри моделі β0 =α, β1 =β.
). Для спрощення запису ми позначаємо параметри моделі β0 =α, β1 =β.
Оскільки на практиці замість генеральної сукупності приходиться мати справу з вибіркою обмеженого обсягу п , вдається одержати засноване на вибіркових даних наближення:yi = a + bxi + ei ; i =1,2,…, n
де параметри а і b моделі є лише деякими оцінками точних значень параметрів α і β. Теоретична залежність (ТЗ) двомірної МЛР (чи апроксимуюча функція f(X, β)) описується рівнянням прямої лінії: у = а+ bх.
Тут множник b називається коефіцієнтом регресії, а величина а - постійної складової лінії регресії.
Коефіцієнт регресії ![]() характеризує збільшення показника при збільшенні фактора на 1 (dx = 1) і має відповідну розмірність. При зміні постійна складової а пряма коллинеарно переміщається, а її розмірність збігається з розмірністю у. Пряма лінія у = а+ bх повинна проходити так, щоб стосовно точок вибірки обсягу п
характеризує збільшення показника при збільшенні фактора на 1 (dx = 1) і має відповідну розмірність. При зміні постійна складової а пряма коллинеарно переміщається, а її розмірність збігається з розмірністю у. Пряма лінія у = а+ bх повинна проходити так, щоб стосовно точок вибірки обсягу п ![]()
забезпечити мінімальну середньоквадратичну помилку (СКП). Метод визначення параметрів моделі з мінімальної СКП називається методом найменших квадратів (МНК чи LSM- Least Squares Method в англомовній літературі).
Безліч точок вибірки ![]() на графіку рис. 1 у декартовых координатах х,у називають діаграмою розсіювання.
на графіку рис. 1 у декартовых координатах х,у називають діаграмою розсіювання.
Для кожної крапки вибірки помилка результату вибірки (залишок регресії) дорівнюєеі = уі - уі * = уі – а - b і
Ця помилка для і-й точки представлена на рис. 2.
 |
 |
Рис. 2.
Середній квадрат помилок апроксимації пропорційний сумі квадратів помилок:![]()
Цю згортку називають функціоналом помилок. Визначимо оцінки а і b параметрів моделі за допомогою методу найменших квадратів (МНК). Його суть складається в мінімізації функціонала помилок при варіаціях параметрів моделі. Тому що а і b поки невідомі, замінимо їх перемінними а→α і b→β. Варіації перемінних α і β дозволять знайти оптимальні за заданим критерієм оцінки.
Функціонал помилок як функція α і β має вид:
![]()
У тривимірному просторі з координатами підстави α і βця функція являє собою поверхню з параболічними перетинами, мал. 3. Абсолютний мінімум параболічної функції при варіації лепеха має місце в точці нульових часток похідних. Для точки абсолютного мінімуму функції ![]() одержимо систему двох лінійних відносно α і β рівнянь:
одержимо систему двох лінійних відносно α і β рівнянь:
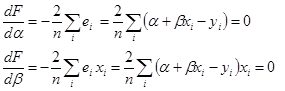
Рішення цієї системи лінійних відносно α і β рівнянь дає оцінки МНК а і b значень параметрів моделі. На мал. 3 вони показані як проекції крапки мінімуму функцій F(a, b) на координатні осі а і bпідстави. Ці оцінки можуть тим більше відрізнятися від точних значень а і b в специфікації моделі, чим менше обсяг вибірки п у порівнянні обсягом генеральної сукупності N. Абсолютна точність оцінок досягається в граничному випадку (п→N, при цьому а→α і b→β). Відзначимо, що за умовами аналізу специфікації моделі а і b- фіксовані параметри, але у функції ми їх розглядаємо варїруємими перемінними для перебування оптимальних вибіркових оцінок а і b.
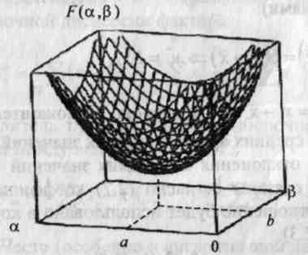
Рис. 3
З попереднього рівняння , зокрема , випливає, що сумарна помилка апроксимації (сума залишків регресії)
![]()
Крім того, це рівняння дає співвідношення між вибірковими середніми арифметичними значеннями фактора X і показника у
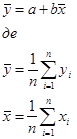
Звідси ясно, що теоретична залежність ТЗ моделі лінійної регресії у = а+ bх, побудована згідно МНК, проходить через точку середніх значень (х,у).
Рішення системи рівнянь щодо α і βмає вид: