Контрольная работа: Побудова лінійної регресійної моделі

Таким чином, загальна дисперсія показника TSS (total sum of squares - загальна сума квадратів) складається з двох складових, що характеризують різні властивості кореляційного полючи даних. Складова ESS (error sum of squares - сума квадратів помилок) характеризує ступінь розкиду точок у, щодо теоретичної прямої і, отже, виражає властивість випадковості вибіркової сукупності. Складова RSS (regressіon sum of squares - сума квадратів регресії), навпроти, пропорційна квадрату різниці між лінією регресії і постійної середній, тобто характеризує властивість закономірності зв'язку. Її частка в загальній дисперсії, обумовлена як коефіцієнт детермінації

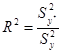
є параметром, що визначає значимість лінійного статистичного зв'язку між фактором і показником. З цього випливає, що

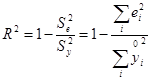
Ця формула зручна при розрахунках, якщо за результатами моделювання обчислені залишки регресії е_і , і їхні квадрати.

Коефіцієнт детермінації можна також виразити через коефіцієнт регресії b , якщо врахувати, що зведення в квадрат і усереднення дає

Тоді

або

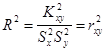
Таким чином, коефіцієнт детермінації дорівнює квадрату коефіцієнта кореляції

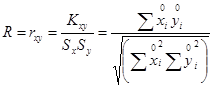
Коефіцієнт кореляції можна виразити через коефіцієнт регресії як:

Таким чином, знак коефіцієнта кореляції збігається зі знаком коефіцієнта регресії b . Останній, однак, відрізняється тим, що може мати розмірність [у/х], тоді як коефіцієнт кореляції R- величина безрозмірна.

Коефіцієнт кореляції характеризує ступінь лінійного статистичного зв'язку. Він приймає значення в інтервалі

- 1 < R < 1.

У крайніх точках R = ± 1 статистичний зв'язок стає лінійним функціональним, позитивним (R = 1) чи негативним (R = - 1). В області R є (0, 1] регресія позитивна (b > 0), а в області r_ху є [- 1, 0) - негативна (b < 0). При R = 0 говорять, що величини Х і Y некорельовані. У теорії імовірності доводиться, що незалежні випадкові величини завжди некорельовані (зворотне твердження вірне лише в окремих випадках, наприклад, для нормальних випадкових величин X і Y). Звичайно думають, що при | R | < 0,3 кореляційний зв'язок слабкий, при | R | - (0,3..0,7) - середній, а при | R | > 0,7 - сильний.

Коефіцієнт кореляції є більш інформативним параметром у порівнянні з коефіцієнтом детермінації, тому що його знак дозволяє судити про позитивну чи негативну кореляцію (і, тим самим, регресії). Відповідно область значень коефіцієнта детермінації

0≤R² ≤1.

Важливою властивістю коефіцієнтів кореляції і детермінації є їхня незалежність від зміни розмірності величин X і (чи) Y, а також від їхньої пропорційної зміни. Скажемо, ми вивчаємо залежність товарообігу Y торгового підприємства від торгової площі X [м² ]. Коефіцієнт регресії b при цьому виміряється в ден. од./м² , наприклад, грн./м² , чи євро/м² . Перехід від однієї одиниці до іншої супроводжується пропорційною зміною коефіцієнта регресії b (а також і постійної складовий а, якщо змінюється показник Y). Разом з тим на коефіцієнти R² і R такі перерахування не впливають, вони є безрозмірними відносними показниками (коефіцієнт R² можна, наприклад, виразити в %).

6. Ступені вільності, аналіз дисперсій

Завжди варто пам'ятати, що однієї з основних задач моделювання є в остаточному підсумку одержати результат прогнозу показника Y для якогось цікавлячого економіста значення фактора х_р (у точці прогнозу). Скажемо, при побудові моделі сімейних витрат на харчування в залежності від числа членів родини у вибірку ввійшли родини до 5 чоловік, а ми хочемо спрогнозувати ці витрати для родини з 7 чоловік (х_р = 7). Середнє значення прогнозу показника в точці прогнозу х_р легко визначається з рівняння моделі:

М[у_р ] = М[а + b х_р + ε_p ] = а + b хр = у_р .

Таким чином, середнє значення прогнозу лежить на прямій, що визначає теоретичну залежність моделі.

Після перебування середнього значення прогнозу завжди виникає традиційне питання: яка точність прогнозу, яка ступінь його надійності. Звичайно для цього залучаються интервальні оцінки помилок моделювання (довірчий інтервал разом з довірчою імовірністю). Для кожного значення прогнозу помилки виявляються різними. Це природно, якщо згадати, що помилки, наприклад, у прогнозі погоди ростуть зі збільшенням часу до точки прогнозу (прогноз на завтра більш точний, чим на тиждень уперед).

Визначимо дисперсію і середньоквадратичну помилку прогнозу показника у_р . У специфікації моделі для відхилень замінимо точку спостереження х, на прогнозну крапку х_р :