Контрольная работа: Побудова лінійної регресійної моделі

Побудувати економетричну модель за наведеними даними. Оцінити параметри моделі. Зробити економічні висновки. Оцінити тісноту та значимість зв’язку між змінними.

Номер підприємства	1	2	3	4	5	6	7
Випуск продукції, тис. шт.	9,33	8,31	8,25	7,50	6,90	6,15	5,66
Витрати матеріалу на од., г. од.	19,66	20,53	21,31	22,59	23,27	24,44	25,85

Рішення :

Номер підприємства	1	2	3	4	5	6	7	Σ
Випуск продукції, тис. шт. х	9,33	8,31	8,25	7,50	6,90	6,15	5,66	52,10
Витрати матеріалу на од., г. од. у	19,66	20,53	21,31	22,59	23,27	24,44	25,85	157,65
	87,0489	69,0561	68,0625	56,25	47,61	37,8225	32,0356	397,8856
	183,4278	170,6043	175,8075	169,425	160,563	150,306	146,311	1156,4446
	1,8871	0,8671	0,8071	0,0571	-0,5429	-1,2929	-1,7829	0
	-2,8614	-1,9914	-1,2114	0,0686	0,7486	1,9186	3,3286	0
	3,5611	0,7519	0,6514	0,0033	0,2947	1,6716	3,1787	10,1127
	8,1876	3,9657	1,4674	0,0047	0,5604	3,681	11,0796	28,9464
	19,3639	21,0706	21,171	22,4259	23,4298	24,6847	25,5046	157,6505
	0,2961	-0,5406	0,139	0,1641	-0,1598	-0,2447	0,3454	0
	2,7626	-4,4924	1,1468	1,2308	-1,1026	-1,5049	1,955	0
	0,0877	0,2922	0,0193	0,0269	0,0255	0,0599	0,1193	0,6308

Середні арифметичні показника і фактора:

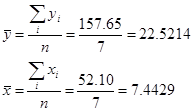
Рівняння моделі лінійної регресії має вигляд: у = а+ b х .

Знайдемо коефіцієнти а і b:

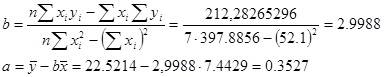
Таким чином, рівняння моделі лінійної регресії має вигляд:

у =0,3527+2,9988×х

Коефіцієнт кореляції характеризує ступень лінійного статистичного зв’язку:

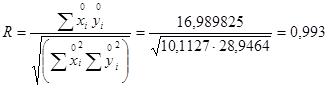
Тобто зв'язок між випуском продукції та витратами матеріалів на одиницю дуже щільний.

Маємо визначені середні значення величин - X_cp = 7,4429, Y_cp = 22,5214, слідові можна визначити середній коефіцієнт еластичності для цієї моделі:

A = b * X_cp / Y_cp = 2,9988*7,4429/22,5214 = 0,991,

тобто при зростанні показника (випуск продукції) на 1% показник Y (витрати матеріалів на одиницю продукції) зростає на 0,99%.

Можна зробити попередні висновки:

В результаті розрахунків отримано модель у^{^} = 0,3527+2,9988×х. Аналізуючи параметри моделі можливо зробити наступні висновки, що оскільки коефіцієнт регресії додатний a₁ =2,9988, то це свідчить про те, що напрямок зв’язку між X і Y прямий (це підтверджує й графік моделі, рис.1), тобто при зростанні Х значення Y теж будуть збільшуватись. При збільшенні Х на 1 значення Y зросте на 0,99.

Рис.1.

Коефіцієнт еластичності свідчить, на скільки відсотків гранично змінюється залежна змінна, якщо відповідна незалежна змінна змінюється на 1%, а інші - постійні.

Коефіцієнт детермінації визначає значимість лінійного статистичного зв’язку між фактором та показником:

, чи

R² = 0,993² = 0,986

По вихідним даним к₁ =к-1=2-1=1 і к₂ =п -к=7-2=5 знаходимо критичне значення коефіцієнта детермінації: R² _кр =0,569.

Так як R² >R² _кр , то можна зробити висновок, що зв'язок між випуском продукції та витратами матеріалів на одиницю статистично значимий з імовірністю 0,95.

Визначимо спостережуване значення критерію Фишера

F = R² *(n - 2)/(1 – R² ) = 0,986*(5)/(1 – 0,986) = 352,14.

Табличне значення критерію при надійності Р=0,95 (a = 0,05) і степенях свободи k₁ = 1, k₂ = 7 – 2 = 5 дорівнює 5,59, оскільки спостережуване значення більше критичного, то лінійна модель є адекватною.

Використовуючи t-статистику, з надійністю Р=0,95 оцінимо значущість коефіцієнта кореляції. Обчислимо спостережуване значення t-статистики

t = |R|*√(n - 2)/(1 – R² ) = 0,993*√(7 - 2)/(1 – 0,986) = 18,766.