Контрольная работа: Проекции и диаграммы

· Дуга полуокружности отобразится на диаграмме в виде ДВУХ отрезков, проходящих через крайние точки линии экватора (то есть, через точки )

· Точки, ограничивающие эти отрезки, так же отображают точки

· Полная длина отрезков так же равна , а точка находится на середине соответствующего отрезка.

Таким образом у нас выходит, что:

· Главный меридиан сферы на цилиндрической диаграмме отобразится ТРЕМЯ ЛИНИЯМИ.

· Каждый полюс сферы , через которые проходит главный меридиан, на диаграмме отобразится ТРЕМЯ точками.

А теперь обобщим. Так как на сфере мы можем провести бесконечное количество меридианов и каждый из них проходит через точки полюсов, то получается, что точки полюсов сферы на диаграмме отобразятся в виде отрезков прямых, соединяющих одноименные точки.

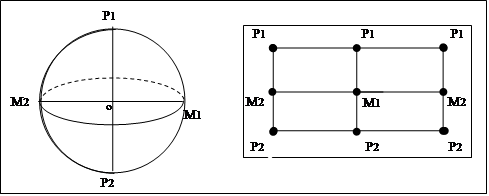
Как мы видим, в отличии от цилиндрической ПРОЕКЦИИ, на которой мы не можем отобразить полюса сферы, на цилиндрической ДИАГРАММЕ полюса сферы отображаются отрезками прямых линий, длина которых равна , хотя в действительности, как мы знаем, ТОЧКА не имеет размеров.

Есть еще одна особенность цилиндрической диаграммы. Эта особенность заключается в том, что МАСШТАБ цилиндрической диаграммы – РАВНОМЕРНЫЙ, то есть область цилиндрической диаграммы можно представить в виде клетчатого листа из школьной тетради.

5. ОТОБРАЖЕНИЕ ПАРАЛЛЕЛЕЙ.

ПАРАЛЛЕЛЬ - это малый круг, полученный от сечения сферы плоскостью, параллельной плоскости экватора. За НУЛЕВУЮ параллель принимается линия экватора. Расстояние параллели от экватора называется ШИРОТОЙ (обозначается как ).

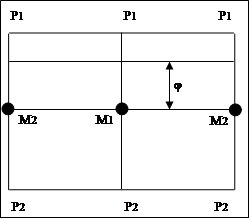
На диаграмме линия параллели отобразится прямой, параллельной линии экватора и отстоящей от линии экватора на расстоянии 

Я думаю Вам понятно, что  изменяется в пределах () или ().

6. ОТОБРАЖЕНИЕ МЕРИДИАНОВ.

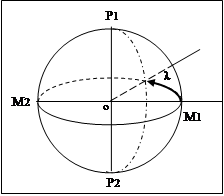
МЕРИДИАН – это большой круг, полученный от сечения сферы центральной плоскостью, проходящей через полярную ось P1 P2. Один из меридианов считается ГЛАВНЫМ (или НУЛЕВЫМ) меридианом. Какой из меридианов считать главным, зависит от конкретной задачи. Расстояние меридиана от главного меридиана называется ДОЛГОТОЙ (обозначается как ).

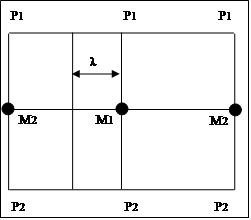
На диаграмме линия меридиана отобразится прямой, параллельной линии главного меридиана.

Долгота  изменяется в пределах ().

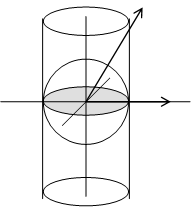
Цилиндрическая проекция

Цилиндрическая проекция - это проекция вписанной в цилиндр сферы, на боковую поверхность цилиндра.

Центром проекционных лучей является центр сферы.

Развернув цилиндр со спроецированной картинкой, мы и получим цилиндрическую проекцию.

При такой проекции приполярные области будут наиболее искажены.

Подготовительная часть