Контрольная работа: Проекции и диаграммы

Начертим две взаимно перпендикулярные линии так, чтобы точка их пересечения (т.О.) находилась ближе к левому нижнему углу чертежа.

Горизонтальная линия называется ЭКВАТОРОМ.

Из точки О, радиусом, равным длине вертикальной линии, проводим дугу до пересечения с линией экватора.

Теперь выбираем ШАГ (), через который будут проходить линии координатной сетки. Чем точнее мы хотим отобразить координатную сетку, тем меньше должен быть шаг, но необходимо помнить, что шаг НЕ МОЖЕТ превышать

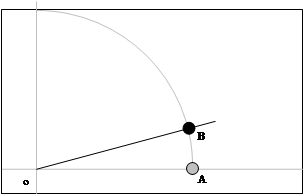
Через т.О, под углом к линии экватора, проведем линию до пересечения с дугой окружности. Обозначим эту точку, как т.В.

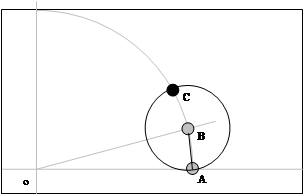
Раствором циркуля, равным длине отрезка АВ, из точки В, как из центра окружности, делаем засечку на ранее построенной дуге. Получаем точку С.

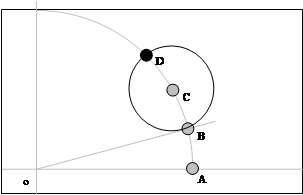
Не изменяя раствора циркуля, уже из т.С, как из центра окружности, делаем засечку на ранее построенной дуге. Получаем точку D.

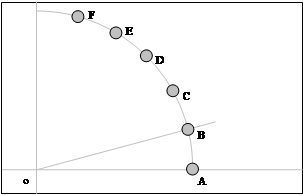
Такие манипуляции мы проделаем столько раз, сколько потребуется, чтобы полностью поделить дугу окружности.

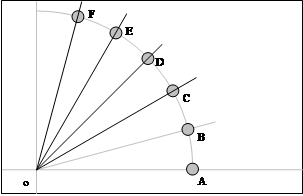
Соединим получившиеся точки с т.О прямыми линиями.

Определим размер чертежа (масштабирование)

Из т.О, как из центра окружности, проводим дугу произвольного радиуса r , Но произвол наш не безграничен. Если мы хотим построить полную цилиндрическую проекцию, то следует помнить, что величина r должна быть равной 1/8 длины экваториальной линии.

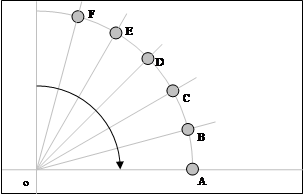
Построение линий проекций меридианов

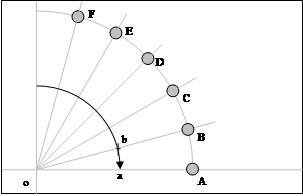
Пересечение дугой радиуса r линии экватора обозначим как точка а .

Пересечение прямой ОВ дуги радиуса r обозначим как точка b .

Расстояние ab - и будет являться ШАГОМ для построения линий проекций меридианов.

На новом листе чертим две взаимно перпендикулярные линии, соблюдая те же условия, которых мы придерживались ранее, т.е. точка пересечения должна находиться в левом нижнем углу чертежа.

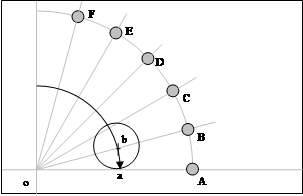
Раствором циркуля, равным расстоянию ab , определенному на вспомогательном чертеже, делаем засечки на линии экватора основного чертежа.