Контрольная работа: Прогноз облікової ставки на основі методу найменших квадратів
б) визначити множинні коефіцієнти детермінації та кореляції:
| номер | у | уі | Е | у-усер. | (у-усер.) в квадраті |
| 1 | 18 | 18,456 | -0,456 | -2,714 | 7,37 |
| 2 | 27 | 17,572 | 12,428 | 9,286 | 86,22 |
| 3 | 10 | 15,762 | -5,762 | -10,714 | 114,80 |
| 4 | 45 | 38,242 | -0,242 | 17,286 | 298,80 |
| 5 | 25 | 21,712 | -0,712 | 0,286 | 0,08 |
| 6 | 11 | 16,202 | -5,202 | -9,714 | 94,37 |
| 7 | 19 | 15,952 | 1,048 | -3,714 | 13,80 |
| Сума | 143,898 | 1,102 | 0,000 | 615,43 | |
| Середнє значення | 22,14 |
R = 1- (1,102/615,43) = 0,998.
Детермінація – D = R2
D = 0,9982 = 0,996
Висновок: рівень рентабельності повністю залежить від сумарних активів та вартості обігових коштів, так як коефіцієнт кореляції склав 1. Таким чином, рівень рентабельності, як результативної ознаки, залежить від факторних ознак (сумарні активи та вартість обігових коштів) на 99,8 відсотка.
в) побудувати точковий та інтервальний прогнози для знайденої моделі.
Вираховується методом підстановки в криву роста величини часу t, тобто в
у = 15,22- 0,02 x1 + 0,82 x2
Завдання 3
0 х 13 (00 х 00001101)
Визначити, використовуючи алгоритм МГОА з послідовним виділенням трендів, часткові описи для другого ряду селекції при наступних даних:
Таблиця 3.1 – Дані про діяльність фірми за минулі роки
| Показники | 1 рік | 2 рік | 3 рік | 4 рік | 5 рік | 6 рік | 7 рік | 8 рік |
|
Попит на продукцію, млн. грн. | 18,2 | 17,6 | 14,2 | 13,8 | 11,5 | 10,1 | 8,1 | 7,2 |
| Ціна, грн. | 24 | 31 | 41 | 51 | 49 | 68 | 77 | 85 |
В якості залежної змінної прийміть попит на продукцію, а незалежних змінних – час, ціну. В якості апроксимуючої функції – лінійну залежність.
Розділимо усю кількість даних (N=8) на дві частини за часом. Перші шість будемо використовувати для розрахунків, а двома останніми (n=2) будемо перевіряти.
Визначимо, який вид залежності найбільш точно описує залежність попиту на продукцію (Y) від незалежних змінних: часу(X1 ) та попиту(X2 ):
y=a0 +a1 x1 ;
y=a0 +a1 x2 ;
y=a0 +a1 x1 +a2 x2 ;
Визначимо лінійну залежність попиту на продукцію від часу. Лінійна залежність має вигляд :
y=a0 +a1 x1 .
Для визначення коефіцієнтів рівняння складемо і розв’яжемо систему :
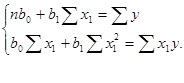
Таблиця 3.2 - Результати проміжних розрахунків
| Рік | х1 (час) | у (попит) | х1 2 | х1 у |
| 1 | 1 | 18,2 | 1,00 | 18,20 |
| 2 | 2 | 17,6 | 4,00 | 35,20 |
| 3 | 3 | 14,2 | 9,00 | 42,60 |
| 4 | 4 | 13,8 | 16,00 | 55,20 |
| 5 | 5 | 11,5 | 25,00 | 57,50 |
| 6 | 6 | 10,1 | 36,00 | 60,60 |
| Сума | 21 | 85,4 | 91 | 269,30 |
Маємо систему:
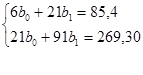
Розв'язавши систему методом підстановки невідомих отримали:
b1 = -1,69