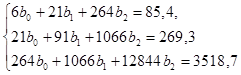Контрольная работа: Прогноз облікової ставки на основі методу найменших квадратів

Залежність попиту на продукцію від часу має вигляд:

У= 20,15 – 1,69х₁ ,

тобто, щороку попит знижується в середньому на 1,69 млн.грн.

Визначимо прогнозні дані на 7 та 8 роки :

У₇ =20,15 – 1,69*7 = 8,32;

У₈ =20,15 – 1,69*8 = 6,63.

Знайдемо середньоквадратичну похибку :

∆₇ =(8,1+8,32)² / 8,1² = 4,11,

∆² ₈ =(7,2+6,63)² / 7,2² = 3,69.

Аналогічно визначимо лінійну залежність попиту на продукцію від ціни:

y=a₀ +a₁ x₂ ;

Рік	х2 (ціна)	у (попит)	х2 2	х2 у
1	24	18,2	576	436,8
2	31	17,6	961	545,60
3	41	14,2	1681	582,2
4	51	13,8	2601	703,8
5	49	11,5	2401	563,50
6	68	10,1	4624	686,8
Сума	264	85,4	12844	3518,7

6b₀ +264b₁ =85,4 b₀ =22,6

264b₀ +12844b₁ = 3518,7, b₁ =-0,19

Розв’язавши методом зрівняння невідомих отримуємо :

y=22,6-0,19x₂ ,

тобто при зростанні ціни на одну гривню попит знижується в середньому на 0,19 млн. грн..

Визначимо прогнозні дані на 7 та 8 років:

y₇ =23,6-0,22*77=6,66;

y₈ =23,6-0,22*85=4,9.

Знайдемо середньоквадратичну похибку:

∆₇ =(77+6,66)² / 6,66² = 157,8,

∆₈ =(85+4,9)² / 4,9² = 336,6.

Визначаємо лінійну залежність попиту від двох факторів: часу та ціни на продукцію. Рівняння, що описує залежність матиме вигляд:

y=a₀ +a₁ x₁ +a₂ x₂ ;

Для визначення параметрів рівняння складемо і розв’яжемо систему нормальних лінійних рівнянь:

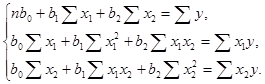
Таблиця 3.4 – результати проміжних розрахунків (незалежні фактори: час, ціна)

Рік	Х1	Х2	У	Х1 2	Х2 2	Х1 Х2	УХ1	УХ2
1	1	24	18,2	1	576	24	18,2	436,8
2	2	31	17,6	4	961	62	35,2	545,6
3	3	41	14,2	9	1681	123	42,6	582,2
4	4	51	13,8	16	2601	204	55,2	703,8
5	5	49	11,5	25	2401	245	57,5	563,5
6	6	68	10,1	36	4624	408	60,6	686,8
Сума	21	264	85,4	91	12844	1066	269,3	3518,7