Контрольная работа: Прогноз облікової ставки на основі методу найменших квадратів
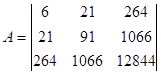
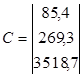
а0 =![]() , а1 =
, а1 =![]() , а2 =
, а2 =![]() .
.
| 6 | 21 | 264 | ||
| D=detA= | 21 | 91 | 1066 | = 7956 |
| 264 | 1066 | 12844 |
| 85,4 | 21 | 264 | ||
| D0 = | 269,3 | 91 | 1066 | = 158238,6 |
| 3518,7 | 1066 | 12844 |
| 6 | 85,4 | 293 | ||
| D1 = | 21 | 269,3 | 1144 | = ‑ 224946,9 |
| 264 | 3518,7 | 15115 |
| 6 | 21 | 85,4 | ||
| D2 = | 21 | 91 | 269,3 | =134,7 |
| 264 | 1066 | 3518,7 |
Визначимо коефіцієнти квадратичної моделі:
а0 = 19,89
а1 = - 28,27
а2 = 0,02
Лінійна залежність попиту на продукцію від часу та ціни має вигляд: y=19,89 - 28,27x1 + 0,02x2 .
Коефіцієнти лінійної багатофакторної моделі показують, що при незмінних цінах щороку попит на продукцію збільшується в середньому на 28,27 млн. грн.. В середині року при зростанні цін на одну гривню, попит на продукцію скорочується в середньому на 0,02 млн. грн..
Визначаємо прогнозні значення та середньоквадратичну похибку:
y7 =19,89-28,27*7+0,02*77= - 176,46;
y8 =19,89-28,27*8+0,02*85= - 204,57;
∆7 =(8,1+176,46)2 / 8,12 = 519,2
∆8 =(7,2+204,57)2 / 7,22 = 865,1
Висновок: залежність попиту на продукцію від часу має найменшу середньоквадратичну похибку, тому слід віддати їй перевагу над іншими. Тому для прогнозування приймаємо наступну модель: y=22,6-0,19x2 .
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1. Горлова В.Л., Мельникова Е.Н. Основы прогнозирования систем - М.: Высш. Шк., 1986.- 287 с.
2. Индуктивный метод самоорганизации моделей сложных систем/ Ивахненко А.Г. – Киев: Наук. Думка, 1981 – 296 с.
3. Лугінін О.Є., Білоусова С.В., Білоусов О.М. Економетрія: Навч. посіб. – К. : Центр навчальної літератури, 2005. – 252 с.
4. Прогнозування фінансової діяльності. Методичні вказівки до самостійної роботи студентів економічних спеціальностей всіх форм навчання / Укл.: Коробко В.І. - Чернігів: ЧДТУ, 2007.- 9 с.