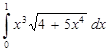Контрольная работа: Производная дифференциал и интеграл

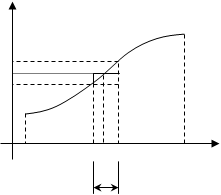
называемую интегральной суммой для функции на отрезке [а , b ]. Геометрический смысл величины s показан на рис. 2.. Это сумма площадей прямоугольников с основаниями и высотами .

При этом числа a и b называются соответственно нижним и верхним пределами , выражение – подынтегральным выражением , – подынтегральной функцией .

Определенный интеграл численно равен площади криволинейной трапеции, ограниченной вертикальными прямыми при , осью Ох и графиком неотрицательной и непрерывной функции . В этом состоит его геометрический смысл.

Если предположить, что – производительность труда в момент t , то будет численно равен объему произведенной продукции за промежуток , т. е. определенному интегралу можно придать экономический смысл.

у В М i m i А О х 0 =а х i х i +1 b = х n х Рис. 2

Предел интегральной суммы при стремлении к нулю, не зависящий от способа выбора точек и точек , называется определенным интегралом от функции на [а , b ] и обозначается

Определенный интеграл обладает рядом свойств, аналогичных свойствам неопределенного интеграла:

1) постоянный множитель можно выносить за знак интеграла;

2) интеграл от алгебраической суммы функций равен такой же сумме интегралов от этих функций (свойство линейности).

Кроме того, определенному интегралу присущи свойства, не имеющие аналогов в теории неопределенных интегралов:

3) интеграл от постоянной величины равен этой постоянной, умноженной на длину отрезка интегрирования

;

4) при перемене местами пределов интегрирования интеграл изменяет лишь знак

;

5) интеграл с одинаковыми пределами интегрирования равен нулю

;

6) для любых чисел а , b и c имеет место равенство

.

Пример. Вычислить определенный интеграл с точностью до двух знаков после запятой