Контрольная работа: Системы линейных алгебраических уравнений

Дана система линейных алгебраических уравнений:

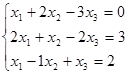
Требуется:

1) Записать матрицу коэффициентов (А) и свободных членов ();

2) Решить систему методом Гаусса и (в случае её невырожденности) Крамера.

Решение.

1) Запишем матрицу коэффициентов:

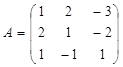
Матрица свободных членов:

2) Решим систему методом Гаусса .

Запишем расширенную матрицу системы и преобразуем её методом Гаусса (приведём к ступенчатому виду с помощью элементарных преобразований строк):

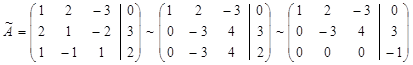
Шаг 1: из строки 2 вычитаем строку 1, умноженную на 2; из строки 3 вычитаем строку 1;

Шаг 2: из строки 3 вычитаем строку 2;

Получили вырожденную систему уравнений, так как если записать уравнение по последней строке преобразованной матрицы, получим 0 = -1, что неверно. Значит, заданная система не имеет решений.

Ответ: решения системы не существует.

Задание №2

Решить матричное уравнение:

АXB^т + m AB = С

, и , m=2.

Решение.

Для того, чтобы решить заданное матричное уравнение, перенесём все известные слагаемые в правую часть, а неизвестные оставим в левой:

Затем обе части уравнения домножим справа на матрицу, обратную к транспонированной матрице В, и домножим слева на матрицу, обратную к матрице А, получим:

где Е – единичная матрица.

Для того, чтобы найти Х, найдём все необходимые матрицы, затем перемножим их.

(*)

Запишем транспонированную матрицу B^т , для чего на место столбцов запишем соответствующие строки:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--