Контрольная работа: Системы линейных алгебраических уравнений

6) Найдём интервалы выпуклости и вогнутости кривой, а также точки её перегиба. Для этого найдём точки, в которой вторая производная меняет знак.

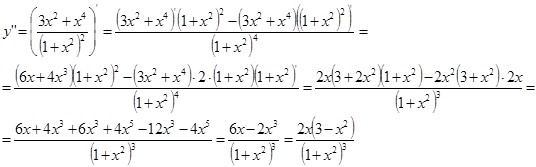
Значит, функция имеет три точки перегиба: .

На каждом из промежутков и вторая производная , следовательно, функция вогнута. На каждом из промежутков и вторая производная , следовательно, функция выпукла.

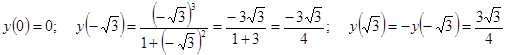
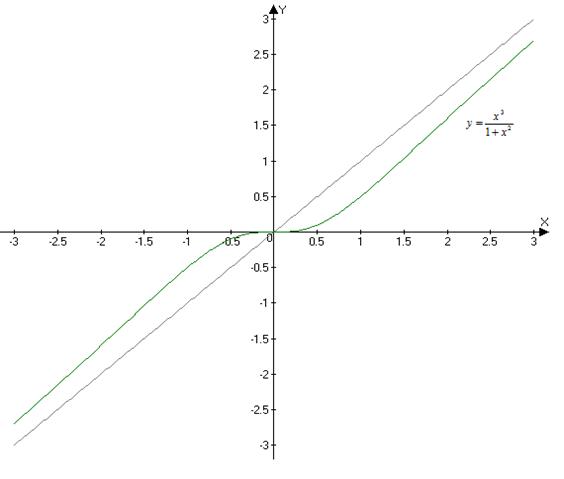
7) Построим график функции

Задание №9

Найти градиент функции в указанной точке:

, М (1,1);

Решение.

Градиент функции в точке находится по формуле:

Вычислим частные производные заданной функции Z и их значения в точке :

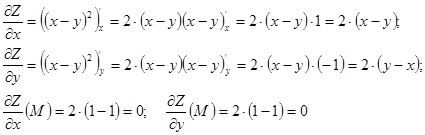
Подставим значения частных производных в точке в формулу для вычисления градиента в точке, получим:

Ответ: .