Контрольная работа: Системы линейных алгебраических уравнений
Вычислим произведение матриц А и В, затем умножим полученную матрицу на m=2:
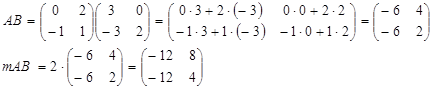
Вычтем полученную матрицу из матрицы С:
![]()
Теперь найдём матрицы ![]() .
.
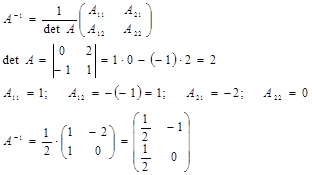
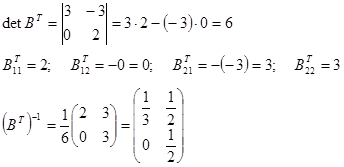
Подставляем все найденные матрицы в уравнение (*)
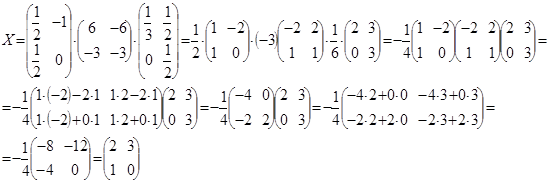
Ответ: ![]() .
.
Задание №3
Даны векторы:![]()
![]() ,
, ![]() и
и ![]() .
.
Требуется:
1) – найти длину вектора ![]() ;
;
2) - вычислить скалярное произведение ![]()
![]() ;
;
3) – найти координаты вектора ![]() ;
;
4) – установить, является ли система векторов ![]() ,
,![]() ,
,![]() линейно зависимой.
линейно зависимой.
Решение.
1) Длина (модуль) вектора ![]() находится по формуле:
находится по формуле:
![]()
Значит, длина вектора ![]() равна:
равна:
![]()
2) Скалярное произведение векторов ![]() и
и ![]() ищется следующим образом:
ищется следующим образом:
![]()
Подставляем координаты векторов ![]() и
и ![]() .
.
![]()
3) Сложение и вычитание векторов заключается в поэлементном соответственно сложении или вычитании их координат. Чтобы умножить вектор на число, необходимо умножить каждую координату вектора на это число. Поэтому:
![]()
Для того, чтобы определить, является ли система из трёх векторов, линейно независимой, достаточно вычислить определитель третьего порядка, составленный из координат этих векторов. Если определитель окажется равным 0, значит, система векторов линейно зависима; если определитель будет отличен от 0 – система векторов линейно независима. Координаты векторов будут строками определителя. Вычислим определитель, разложив его по первому столбцу.