Контрольная работа: Системы линейных алгебраических уравнений

Решение.

Эластичность функции y относительно переменной х вычисляется по формуле

Вычислим производную функции q по p и подставим наши значения в формулу:

Подставим значение , тогда получим:

Полученное значение эластичности спроса по цене показывает, что если цена увеличится на 1%, то спрос снизится на %.

Ответ: .

Задание №8

Исследовать функцию и построить ее график:

Решение.

1) Область определения функции

2) Функция не является периодической.

Функция является нечётной, так как

3) Так как функция нечётна, значит точка пересечения с осью Оу – это начало координат, т.е. точка (0; 0).

Точки пересечения с осью Ох: ,т.е. только точка (0; 0).

4) y(x) непрерывна на всей области определения D(x), значит точек разрыва нет, вертикальных асимптот нет.

Так как пределы бесконечны, значит, горизонтальных асимптот нет.

Найдём наклонные асимптоты вида , если они есть:

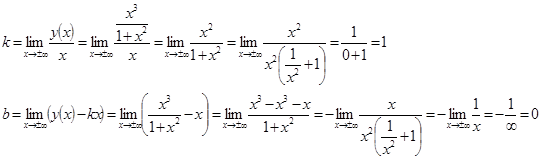
Прямая будет наклонной асимптотой.

5) Найдём экстремумы функции и интервалы возрастания и убывания. Для этого найдём точки, в которых первая производная обращается в 0:

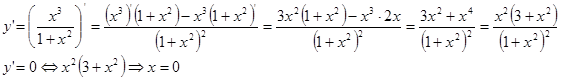
Т.е. критической является точка .

Но в точке x=0, производная не меняет знак, поэтому эта точка не является точкой экстремума.