Контрольная работа: Сходимость рядов
Ряд будет сходиться при ![]() .
.
1)
![]()
в интервале ![]() ряд сходится.
ряд сходится.
2)
![]()
в интервале 3<x<8 ряд сходится.
Общий интервал сходимости –2<x<8.
На концах интервала х=-2, имеем ряд:
![]()
— расходящийся гармонический ряд.
![]()
в п.9.3.1 б) показано, что ряд сходится условно.
Ответ: (-2,8]
9.3.3.
а)
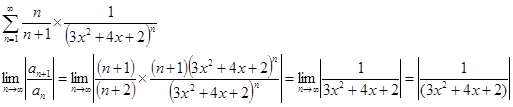
Ряд сходится при условии ![]()
1) ![]()
Решим неравенство:
![]()
корней нет, следовательно: ![]() — всегда.
— всегда.
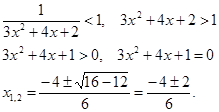
![]()
Ветви параболы направлены вверх, получаем два интервала: ![]() Здесь ряд сходится.
Здесь ряд сходится.
Исследуем концы интервалов:
1) ![]() . Получаем ряд:
. Получаем ряд: 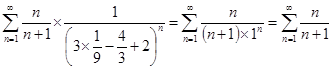 . Ряд расходится, т.к. все его члены не меньше расходящегося гармонического ряда
. Ряд расходится, т.к. все его члены не меньше расходящегося гармонического ряда ![]() .
.
2)
