Контрольная работа: Сходимость рядов

Получим такой же ряд, но члены имеют обратные знаки.

.

9.3.7.

а)

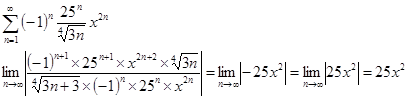
Проверяем концы интервалов

1)

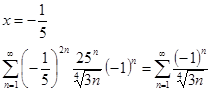
Признак Лейбница выполняется, ряд сходится.

При получится такой же ряд (т.к. x в четной степени).

б)

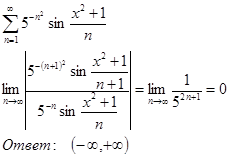
9.3.8.

а)

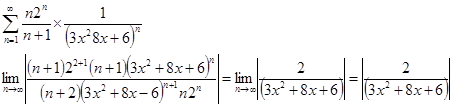
Условие сходимости .

Найдем дискриминант знаменателя: D=64-72<0. Условие принимает вид

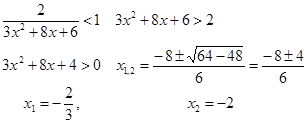
Интервал сходимости .

На концах интервала

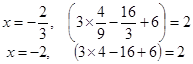
Получаем один и тот же ряд

.

Члены этого ряда не меньше членов ряда , следовательно, ряд расходится.

б)

Условие сходимости