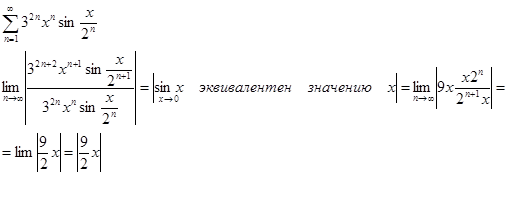Контрольная работа: Сходимость рядов

На краях интервалов:

1) . Получается ряд:

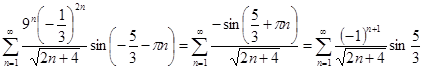
Ряд знакочередующийся, по признаку Лейбница сходится.

2)

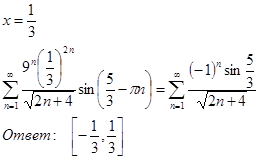
9.3.9.

а)

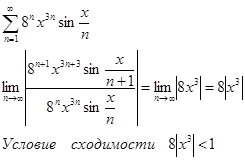
1. Если , т.е. и необходимо решить неравенство: . Получается интервал .

2.

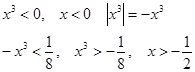
Интервал с учетом .

На концах интервала:

1)

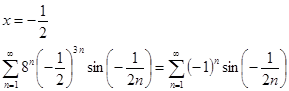
Ряд сходится. Аналогично при .

.

б)

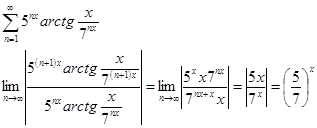
Интервал сходимости определяется неравенством

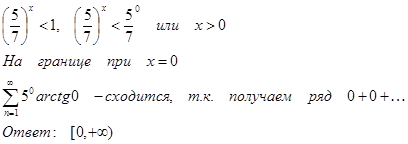
9.3.10.

а)

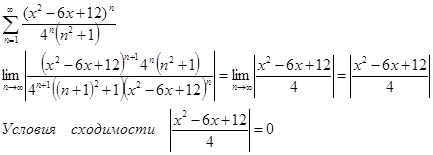
Найдем дискриминант числителя

б)