Контрольная работа: Составление и решение уравнений линейной регрессии
Задача 1
По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (
, млн. руб.) от объема капиталовложений (
, млн. руб.)
Требуется:
1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.
2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков 
; построить график остатков.
3. Проверить выполнение предпосылок МНК.
4. Осуществить проверку значимости параметров уравнения регрессии с помощью t‑критерия Стьюдента 
5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью 
- критерия Фишера 
, найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
6. Осуществить прогнозирование среднего значения показателя при уровне значимости 
, если прогнозное значения фактора Х составит 80% от его максимального значения.
7. Представить графически: фактические и модельные значения 
точки прогноза.
8. Составить уравнения нелинейной регрессии:
· гиперболической;
· степенной;
· показательной.
Привести графики построенных уравнений регрессии.
9. Для указанных моделей найти коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.
 | 17 | 22 | 10 | 7 | 12 | 21 | 14 | 7 | 20 | 3 |
 | 26 | 27 | 22 | 19 | 21 | 26 | 20 | 15 | 30 | 13 |
Решение
1. Уравнение линейной регрессии имеет вид: y = a + b * x .
Данные, используемые для расчета параметров a иb линейной модели, представлены в табл. 1:
Таблица 1
| n | х | у | ух | хх | y-ycp | (у-уср )2 | х-хср | (х-хср )2 | Упр | ε | ε2 | εt -ε t-1 | (εt -ε t-1 )2 |
| 1 | 17 | 26 | 442 | 289 | 4,1 | 16,81 | 3,7 | 13,69 | 27,71 | 1,71 | 2,92 | ||
| 2 | 22 | 27 | 594 | 484 | 5,1 | 26,01 | 8,7 | 75,69 | 32,26 | 5,26 | 27,67 | 3,55 | 12,60 |
| 3 | 10 | 22 | 220 | 100 | 0,1 | 0,01 | -3,3 | 10,89 | 21,34 | -0,66 | 0,44 | -5,92 | 35,05 |
| 4 | 7 | 19 | 133 | 49 | -2,9 | 8,41 | -6,3 | 39,69 | 18,61 | -0,39 | 0,15 | 0,27 | 0,07 |
| 5 | 12 | 21 | 252 | 144 | -0,9 | 0,81 | -1,3 | 1,69 | 23,16 | 2,16 | 4,67 | 2,55 | 6,50 |
| 6 | 21 | 26 | 546 | 441 | 4,1 | 16,81 | 7,7 | 59,29 | 31,35 | 5,35 | 28,62 | 3,19 | 10,18 |
| 7 | 14 | 20 | 280 | 196 | -1,9 | 3,61 | 0,7 | 0,49 | 24,98 | 4,98 | 24,80 | -0,37 | 0,14 |
| 8 | 7 | 15 | 105 | 49 | -6,9 | 47,61 | -6,3 | 39,69 | 18,61 | 3,61 | 13,03 | -1,37 | 1,88 |
| 9 | 20 | 30 | 600 | 400 | 8,1 | 65,61 | 6,7 | 44,89 | 30,44 | 0,44 | 0,19 | -3,17 | 10,05 |
| 10 | 3 | 13 | 39 | 9 | -8,9 | 79,21 | -10,3 | 106,09 | 14,97 | 1,97 | 3,88 | 1,53 | 2,34 |
| сумма | 133 | 219 | 3211 | 2161 | 264,90 | 392,1 | 24,43 | 106,37 | 0,26 | 78,80 | |||
| ср. знач. | 13,3 | 21,9 | 321,1 | 216,1 |
;
Уравнение линейной регрессии имеет вид: у= 11,78+0,76х
С увеличением объема капиталовложений на 1 млн. руб. объем выпускаемой продукции увеличится в среднем на 76 тыс. руб. Это свидетельствует об эффективности работы предприятия.
2. Вычисленные остатки и остаточная сумма квадратов представлены в таблице 1. Дисперсию остатков оценим по формуле:
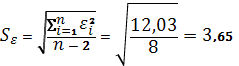– стандартная ошибка оценки.Построим график остатков (рис. 1)
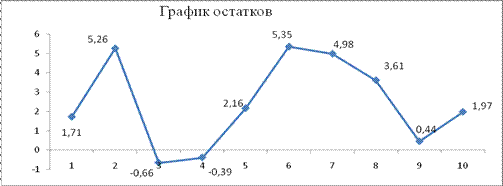
Рисунок 1
--> ЧИТАТЬ ПОЛНОСТЬЮ <--