Контрольная работа: Составление и решение уравнений линейной регрессии
Независимость остатков проверяется с помощью критерия Дарбина – Уотсона по формуле ![]() , т. к.
, т. к. ![]() =0,74, d1 =1,08, d2 =1,36, т.е. d<d1 , значитряд остатковсодержит автокорреляцию.
=0,74, d1 =1,08, d2 =1,36, т.е. d<d1 , значитряд остатковсодержит автокорреляцию.
Для обнаружения гетероскедастичности используем тест Голдфельда – Квандта:
1) Упорядочим наблюдения по мере возрастания переменной х.
2) Разделим совокупность на 2 группы по 5 наблюдений и для каждой определим уравнение регрессии. Воспользуемся инструментом Регрессия пакета Анализ данных, полученные результаты представлены в табл. 2.
Таблица 2
| n | у1 | Предсказанное у1 | е1 | е12 | у2 | Предсказанное у2 | е2 | е22 |
| 1 | 13 | 13,81 | -0,81 | 0,66 | 22 | 22,46 | -0,46 | 0,21 |
| 2 | 15 | 16,52 | -1,52 | 2,30 | 26 | 25,73 | 0,27 | 0,07 |
| 3 | 19 | 16,52 | 2,48 | 6,16 | 26 | 27,60 | -1,60 | 2,57 |
| 4 | 20 | 21,25 | -1,25 | 1,57 | 27 | 28,07 | -1,07 | 1,15 |
| 5 | 21 | 19,90 | 1,10 | 1,21 | 30 | 27,14 | 2,86 | 8,20 |
| сумма | 11,90 | 12,20 |
3) Определим остаточную сумму квадратов для первой ![]() и второй регрессии
и второй регрессии ![]() .
.
4) Вычислим отношение 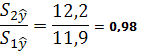 , т. к. Fнабл =0,98, Fкр(α,к1,к2) = Fкр(0,05,5,5) =5,05 (из таблицы критерия Фишера), Fнабл <Fкр, то гетероскедастичность отсутствует, предпосылка о равенстве дисперсий остаточных величии не нарушена.
, т. к. Fнабл =0,98, Fкр(α,к1,к2) = Fкр(0,05,5,5) =5,05 (из таблицы критерия Фишера), Fнабл <Fкр, то гетероскедастичность отсутствует, предпосылка о равенстве дисперсий остаточных величии не нарушена.
4. Проверим значимость параметров уравнения регрессии с помощью t‑критерия Стьюдента ![]() Расчетные значения t‑критерия Стьюдента для коэффициента уравнения регрессии а1 приведены в четвертом столбце протокола Excel, полученном при использовании инструмента Регрессия (рис. 2).
Расчетные значения t‑критерия Стьюдента для коэффициента уравнения регрессии а1 приведены в четвертом столбце протокола Excel, полученном при использовании инструмента Регрессия (рис. 2).
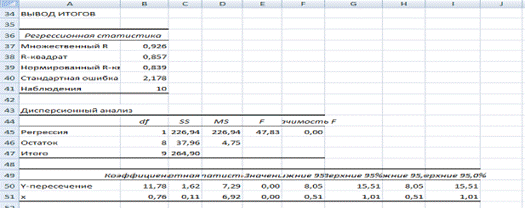
Рисунок 2
Табличное значение t‑критерия Стьюдента 2,30. tрасч =6,92, так как tрасч >tтабл , то коэффициент а1 значим.
5. Значение коэффициента детерминации (R – квадрат) можно найти в таблице Регрессионная статистика (рис. 2). Коэффициент детерминации/ Он показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, около 85,7% вариации зависимой переменной (объем выпуска продукции) учтено в модели и обусловлено влиянием включенного фактора (объем капиталовложений).
Значение F– критерия Фишера можно найти в таблице протокола Excel (рис. 2), Fрасч =47,83. Табличное значение F– критерия при доверительной вероятности 0,05 равно 4,46, т. к. Fрасч >Fтабл , уравнение регрессии следует признать адекватным.
Определим среднюю относительную ошибку аппроксимации? в среднем расчетные значения у для линейной модели отличаются от фактических на 1% – хорошее качество модели.
6. Осуществим прогнозирование среднего значения показателя ![]() при уровне значимости
при уровне значимости ![]() , если прогнозное значения фактора Х составит 80% от его максимального значения.
, если прогнозное значения фактора Х составит 80% от его максимального значения.
Модель зависимости объема выпуска продукции от величины капиталовложений у= 11,78+0,76х. Для того чтобы определить среднее значение фактора У при 80% максимального значения фактора Х, необходимо подставить Хпрогн =Хmax *0,8=22*0,8=17,6 в полученную модель: Упрогн =11,78+0,76*17,6=25,17
Для построения интервального прогноза рассчитаем доверительный интервал. Критерий Стьюдента (при v=n -2=10–2=8) равен 1,8595. Ширину доверительного интервала вычислим по формуле:
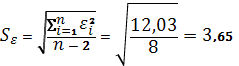
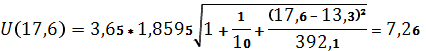 ,
,
таким образом, прогнозное значение будет находиться между:
Yпрогн(80 % max ) += 25,17+7,26=32,43 – верхняя граница прогноза,
Yпрогн(80 % max ) – =25,17–7,26=17,91 – нижняя граница прогноза.
7. Графическое представление (рис. 3) модели парной регрессии зависимости объема выпуска продукции от объема капиталовложений: фактические и модельные значения ![]() точки прогноза.
точки прогноза.
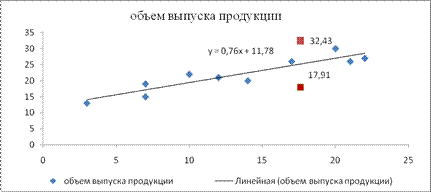
Рисунок 3
8. Уравнение гиперболической функции: y = a + b / x . Произведем линеаризацию путем замены Х=1/х . В результате получим линейное уравнение y = a + b Х. Рассчитаем его параметры по данным таблицы 3
Таблица 3
| n | х | у | Х | уХ | Х2 | y-ycp | (у-уср )2 | Упр | ε | ε2 | /ε/у/*100% |
| 1 | 17 | 26 | 0,05882 | 1,52941 | 0,0035 | 4,1 | 16,81 | 24,3846 | 1,62 | 2,61 | 6,213 |
| 2 | 22 | 27 | 0,04545 | 1,22727 | 0,0021 | 5,1 | 26,01 | 25,066 | 1,93 | 3,74 | 7,163 |
| 3 | 10 | 22 | 0,10000 | 2,20000 | 0,0100 | 0,1 | 0,01 | 22,2859 | -0,29 | 0,08 | 1,299 |
| 4 | 7 | 19 | 0,14286 | 2,71429 | 0,0204 | -2,9 | 8,41 | 20,1015 | -1,10 | 1,21 | 5,797 |
| 5 | 12 | 21 | 0,08333 | 1,75000 | 0,0069 | -0,9 | 0,81 | 23,1354 | -2,14 | 4,56 | 10,168 |
| 6 | 21 | 26 | 0,04762 | 1,23810 | 0,0023 | 4,1 | 16,81 | 24,9557 | 1,04 | 1,09 | 4,016 |
| 7 | 14 | 20 | 0,07143 | 1,42857 | 0,0051 | -1,9 | 3,61 | 23,7422 | -3,74 | 14,00 | 18,711 |
| 8 | 7 | 15 | 0,14286 | 2,14286 | 0,0204 | -6,9 | 47,61 | 20,1015 | -5,10 | 26,02 | 34,010 |
| 9 | 20 | 30 | 0,05000 | 1,50000 | 0,0025 | 8,1 | 65,61 | 24,8344 | 5,17 | 26,68 | 17,219 |
| 10 | 3 | 13 | 0,33333 | 4,33333 | 0,1111 | -8,9 | 79,21 | 10,3929 | 2,61 | 6,80 | 20,054 |
| сумма | 219 | 20,0638 | 0,1843 | 265 | 219 | 0,00 | 86,80 | 124,65 | |||
| ср. знач. | 13,3 | 21,9 | 0,10757 | 2,00638 | 0,0184 | 12,465 |
![]() ,
,
получим следующее уравнение гиперболической модели: ỹ =27,38–50,97/х .