Экономико-математическое моделирование / Контрольная работа: Составление и решение уравнений линейной регрессии

Контрольная работа: Составление и решение уравнений линейной регрессии

Таблица 4

n у Y=lg(y) х X=lg(x) YX X2 yпр ε ε2 |ε/y|*100%
1 26 1,415 17 1,230 1,741 1,514 24,823 1,177 1,385 0,045
2 27 1,431 22 1,342 1,921 1,802 27,476 -0,476 0,226 0,018
3 22 1,342 10 1,000 1,342 1,000 20,142 1,858 3,452 0,084
4 19 1,279 7 0,845 1,081 0,714 17,503 1,497 2,242 0,079
5 21 1,322 12 1,079 1,427 1,165 21,641 -0,641 0,411 0,031
6 26 1,415 21 1,322 1,871 1,748 26,977 -0,977 0,955 0,038
7 20 1,301 14 1,146 1,491 1,314 22,996 -2,996 8,975 0,150
8 15 1,176 7 0,845 0,994 0,714 17,503 -2,503 6,263 0,167
9 30 1,477 20 1,301 1,922 1,693 26,464 3,536 12,505 0,118
10 13 1,114 3 0,477 0,531 0,228 12,537 0,463 0,214 0,036
сумма 219 13,273 10,589 14,322 11,891 0,939 36,630 0,764
ср. знач. 1,327 1,059 1,432 1,189 0,076

Уравнение регрессии будет иметь вид: У=0,9103+0,3938*Х. Перейдем к исходным переменным х и у, выполнив потенцирование данного уравнения: ỹ=100,9103 *х0,3938 .

Получим уравнение степенной модели регрессии: ỹ=8,1339*х0,3938 .

Уравнение показательной кривой: ỹ=а*bx . Осуществим логарифмирование обеих частей уравнения: lgy=lg a +x*lgb . Обозначим Y=lgy', В=lgb, A=lga. Получим линейное уравнение регрессии: Y=A+Вх . Рассчитаем его параметры, используя данные табл. 5

Таблица 5

n у Y=lg(y) х Ух х2 У-Уср (У-Уср )2 х-хср (х-хср )2 Упр ε ε2 |ε/y|*100%
1 26 1,415 17 24,0545 289 0,088 0,008 3,7 13,69 24,365 1,635 2,673 26
2 27 1,431 22 31,49 484 0,104 0,011 8,7 75,69 29,318 -2,318 5,375 27
3 22 1,342 10 13,4242 100 0,015 0,000 -3,3 10,89 18,804 3,196 10,21 22
4 19 1,279 7 8,95128 49 -0,049 0,002 -6,3 39,69 16,827 2,173 4,720 19
5 21 1,322 12 15,8666 144 -0,005 0,000 -1,3 1,69 20,248 0,752 0,565 21
6 26 1,415 21 29,7144 441 0,088 0,008 7,7 59,29 28,253 -2,253 5,076 26
7 20 1,301 14 18,2144 196 -0,026 0,001 0,7 0,49 21,804 -1,804 3,255 20
8 15 1,176 7 8,23264 49 -0,151 0,023 -6,3 39,69 16,827 -1,827 3,339 15
9 30 1,477 20 29,5424 400 0,150 0,022 6,7 44,89 27,226 2,774 7,693 30
10 13 1,114 3 3,34183 9 -0,213 0,046 -10,3 106,09 14,512 -1,512 2,285 13
сумма 219 13,273 133 182,832 2161 0,120 392,1 0,814 45,199 219
ср. зн 1,327 13,3 18,2832 216,1

Уравнение имеет вид: У=1,11+0,0161х . Перейдем к исходным переменным х и у , выполнив потенцирование уравнения:

ỹ =101,11 (10 0,0161 )х , ỹ =12,99*1,038х – уравнение показательной кривой.

Графики построенных уравнений регрессии приведены на рис. 4.

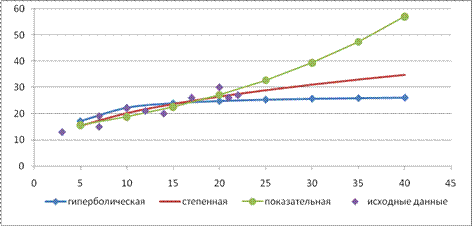
Рисунок 4

9. Коэффициент детерминации:

Для сравнения и выбора лучшей модели строим сводную таблицу результатов (табл. 6).


Таблица 6

Параметры

Модель

 коэффициент детерминации средняя относительная ошибка аппроксимации коэффициент эластичности
гиперболическая 0,672 7,257 -0,250
степенная 0,862 0,034 0,239
показательная 0,829 3,82 0,010

Вывод: на основании полученных данных лучшей является степенная модель регрессии, т. к. она имеет наибольший коэффициент детерминации R2 =0,862, т.е. вариация факторного признака У (объем выпуска продукции) на 86,2% объясняется вариацией фактора Х (объемом капиталовложений), и наименьшую относительную ошибку (в среднем расчетные значения для степенной модели отличаются от фактических данных на 0,034%). Также степенная модель имеет наибольший коэффициент эластичности, т.е. при изменении фактора на 1% зависимая переменная изменится на 0,24%, таким образом степенную модель можно взять в качестве лучшей для построения прогноза.

Задача 2а и 2б

Имеются два варианта структурной формы модели, заданные в виде матриц коэффициентов модели. Необходимо для каждой матрицы записать системы одновременных уравнений и проверить их на идентифицируемость.

Задача 2а

Решение.

Запишем систему одновременных уравнений:

у1= b 12 у2+ b 13 у3+ a 12 х2+ a 13 х3

у2= b 23 у3+ a 21 х1+ a 22 х2+ a 24 x4

у3 = b 32 у2+ a 31 х1+ a 32 х2+ a 33 х3

Проверим каждое уравнение на выполнение необходимого и достаточного условия идентификации.

1) В первом уравнении три эндогенные переменные у1, у2, у3 (Н=3). В нем отсутствуют экзогенные переменные х1, х4 (D=2). Необходимое условие идентификации D+1=H, 2+1=3 выполнено.

Для проверки на достаточное условие составим матрицу из коэффициентов при переменных х1 и х4 (табл. 7)

Таблица 7

Уравнения, из которых взяты коэффициенты при переменных Переменные
х1 х4
2 a 21 a 24
3 a 31 0

Определитель матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, первое уравнение идентифицируемо.

К-во Просмотров: 369
Бесплатно скачать Контрольная работа: Составление и решение уравнений линейной регрессии