4. Установлюють нормативне відхилення t, значення якого задають, наприклад при великій точності вимірювань t=3.0, при малій – t=2.0, можна прийняти t=2.5.

5. Із (6.26) визначають . В процесі експерименту число вимірів не повинно бути менше .

Приклад

при прийманні споруди, комісія в якості одного із параметрів, вимірює її ширину. Необхідно виконати 25 вимірів, допустиме відхилення параметра м. Необхідно визначити, з якою вірогідністю комісія оцінює даний параметр. Попереднє обчислення значення м.

Допустиме відхилення параметра м. з рівняння (6.27) запишемо . ; . У відповідності з таблицею (6.). Надійна ймовірність для це низька ймовірність. Похибка перевищує надійний інтервал м, згідно формули (6.) ,буде зустрічатися один раз із , тобто із чотирьох вимірювань. Це не допустимо. Вирахуємо мінімальну кількість вимірів, з надійною ймовірністю Р_Д , рівною 0,9 і 0,95. За формулою (6.27) маємо виміри при Р_Д =0,90 і 64 виміри при Р_Д =0,95. Результати вимірювань за допомогою і справедливі при . Для знаходження границь надійного інтервалу при малих значеннях застосовують метод запропонований в 1908 році англійським математиком

В.С. Гессетом (псевдонім Стьюдент). Криві розподілення Стьюдента у разі переходять в криві нормального розпреділення (рис. 6.1).

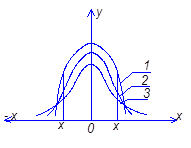
Для малої вибірки надійний інтервал

(6.28)

де - коефіцієнт Стьюдента, який приймається з табл. 6.2 в залежності від значення надійної ймовірності Ф_ст знаючи m_ст , можна визначити дійсне значення величини, що вивчається для малої вибірки:

(6.29).

Можлива інша постановка задачі. Маючи n відомих вимірів малої вибірки необхідно визначити необхідну ймовірність Р_Д за умовою, що похибка середнього значення не вийде за межі .

Задачу розв’язують у такій послідовності:

1. Визначають середнє значення , і .

2. За допомогою величини , відомого n і таблиці 6.2 визначають надійну ймовірність.

Інтегральна формула Лапласа

Надійним називається інтервал значень х_і у який попадає правдиве значення х_д величини, що вимірюється, попадає в даний інтервал.

Надійною ймовірністю ( вірогідністю) вимірювання називається імовірністю Р_д того, що правдиве значення х_д величини, що вимірюється попадає в даний надійний інтервал.

Ця величина визначається в долях одиниці або в процентах. Необхідно встановити ймовірність того, що х_д попаде в зону а<x_д <в. Надійна імовірність Р_д описується виразом:

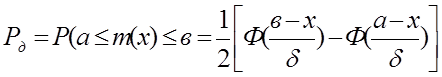(6.30)

де Ф_(t) – функція Лапласса, аргументом якої є відношення µ до середньоквадратичного σ, тобто

t=µ/ σ (6.31)

µ=b-x; µ= - (a-x), t – гарантований коефіцієнт.

Функція Ф(t) – це інтегральна функція Лапласа:

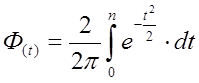(6.32)

Її можна записати так:

(6.33)

Числові значення Ф_(t), приведені в додатку табл. I.

Коли задані межі появи події А(m₁ i m₂ ), які відрізняються від np на [x], то інтегральна формула Лапласа набуде такого вигляду:

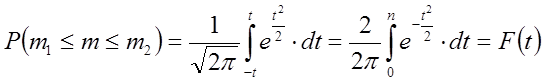(6.34)