Контрольная работа: Теория вероятности

Р1 = 0,8*0,9 = 0,72 (72% продукции)

2) Найдем вероятность того, что нестандартная продукция будет признана годной:

Р2 = 0,2*0,3 = 0,06 (6% продукции)

3) Таким образом, упрощенный контроль признает годной Р1 + Р2 = 0,82 (82% продукции)

4) Найдем вероятность того, что признанное годным изделие - стандартно:

0,8*0,82 = 0,656

Ответ: вероятность того, что признанное годным изделие - стандартно, равна 0,656.

Задача № 5

Условие:

Имеется 4 радиолокатора. Вероятность обнаружить цель для первого - 0,86; для второго - 0,9; для третьего - 0,92; для четвертого - 0,95. Включен один из них. Какова вероятность обнаружить цель?

Решение:

Обозначим через А событие - цель обнаружена, а возможные события (гипотезы) обнаружения цели 1-м, 2-м, 3-м или 4-м локаторами - через, соответственно, В₁ , В₂ , В₃ и В₄ .

По условию задачи включен один из четырех локаторов, следовательно, вероятность обнаружения цели:

Р (В₁ ) = Р (В₂ ) = Р (В₃ ) = Р (В₄ ) = 1\4.

Соответствующие условные вероятности (по условию задачи) обнаружения цели равны:

Р (A|В₁ ) = 0,86; Р (A|В₂ ) = 0,9; Р (A|В₃ ) = 0,92; Р (A|В₄ ) = 0,95.

Таким образом, согласно формуле полной вероятности, искомая вероятность обнаружения цели равна:

Ответ: вероятность обнаружения цели равна 0,9075

Контрольная работа № 2

Вариант 1.

Задача № 1.

Условие:

Известна вероятность события А: р (А) = 0,3. Дискретная случайная величина x - число появлений А в трех опытах. Построить ряд распределения случайной величины x; найти ее математическое ожидание m _x и дисперсию D _x .

Решение:

1) Вычислим вероятности р (х _i ) по формуле Бернулли:

, где, р = 0,3; q = 1 - р = 0,7; n = 3; х = x.

Таким образом, получим ряд распределения случайной величины x:

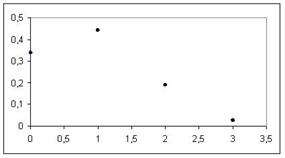
Значения x	0	1	2	3
Вероятности р (х i )	0,343	0,441	0,189	0,027

Графически ряд распределения случайной величины x выглядит следующим образом: