Контрольная работа: Теория вероятности

Определить частные, условные (при x = 1, h = 0) распределения и числовые характеристики системы случайных величин m_x , D_x , m_h , D_h , K_{x, h} , r_{x, h} ; а также найти вероятность попадания двумерной случайной величины (x, h) в область

.

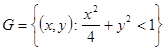Решение:

Частное распределение для x получается суммированием вероятностей в столбцах:

Р (x = 1) = Р (x = 1, h = 0) + Р (x = 1, h = 1) + Р (x = 1, h = 2) = 0,16 + 0,08 + 0,06 = 0,3

Р (x = 2) = Р (x = 2, h = 0) + Р (x = 2, h = 1) + Р (x = 2, h = 2) = 0,12 + 0,10 + 0,04 = 0,26

Р (x = 3) = Р (x = 3, h = 0) + Р (x = 3, h = 1) + Р (x = 3, h = 2) = 0,14 + 0,09 + 0,03 = 0,26

Р (x = 4) = Р (x = 4, h = 0) + Р (x = 4, h = 1) + Р (x = 4, h = 2) = 0,08 + 0,08 + 0,02 = 0,18

Частное распределение для h получается суммированием вероятностей в строках:

Р (h = 0) = Р (h = 0, x = 1) + Р (h = 0, x = 2) + Р (h = 0, x = 3) + Р (h = 0, x = 4) = 0,16 + 0,12 + 0,14 + 0,08 = 0,5

Р (h = 1) = Р (h = 1, x = 1) + Р (h = 1, x = 2) + Р (h = 1, x = 3) + Р (h = 1, x = 4) = 0,08 + 0,10 + 0,09 + 0,08 = 0,35

Р (h = 2) = Р (h = 2, x = 1) + Р (h = 2, x = 2) + Р (h = 2, x = 3) + Р (h = 2, x = 4) = 0,06 + 0,04 + 0,03 + 0,02 = 0,15

Полученные данные можно представить в виде таблицы:

x h	1	2	3	4
0	0,16	0,12	0,14	0,08	0,5
1	0,08	0,10	0,09	0,08	0,35
3	0,06	0,04	0,03	0,02	0,15
0,3	0,26	0,26	0,18

Вычислим математическое ожидание m_x :

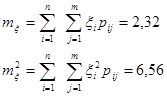
Вычислим математическое ожидание m_h :

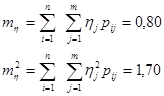
Вычислим дисперсию D_x :

Вычислим дисперсию D_h :

Условное распределение x/h=0:

x	1	2	3	4

Условное распределение h/x=1:

x	0	1	3

Вычислим ковариацию K_{x, h} :

Вычислим коэффициент корреляции r_{x, h} :