Контрольная работа: Типовой расчет

3. Исследовать ряд на сходимость

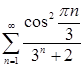
Решение.

Так как , то рассмотрим ряд

, тогда

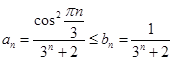
Воспользуемся признаком Даламбера.

,

Тогда,

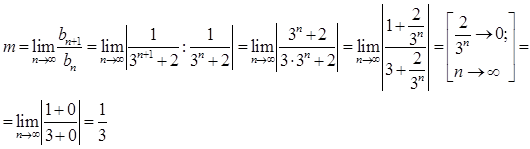
Так как , то ряд сходится. Значит, исходный ряд 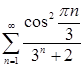сходится по теореме о сравнении рядов.

Ответ: Ряд 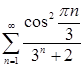сходится.

4. Исследовать ряд на сходимость

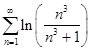
Решение.

Преобразуем n – член этого ряда.

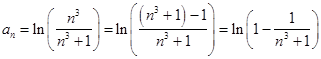
Сравним ряд с рядом , пользуясь предельным признаком сравнения:

,

Тогда,

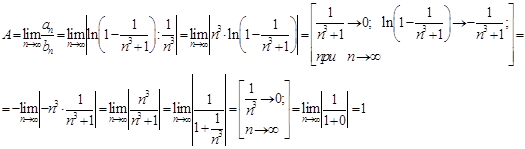
Поскольку А = 1 (0<A<+∞) – действительное число. Следовательно, ряды либо сходятся, либо расходятся. Ряд - является рядом Дирихле. Так как α = 3 > 1, то данный ряд сходится. Следовательно, и сравниваемый ряд 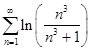тоже сходится.

Ответ: ряд 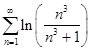сходится.

5. Исследовать ряд на сходимость

Решение.

Воспользуемся признаком Даламбера.

,

Находим m по формуле: