Контрольная работа: Типовой расчет
2) ![]()
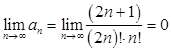
Следовательно, ряд 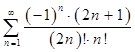 условно сходится.
условно сходится.
Проверим абсолютную сходимость ряда 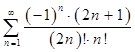 . Рассмотрим ряд
. Рассмотрим ряд ![]() .
.
Воспользуемся признаком Даламбера:
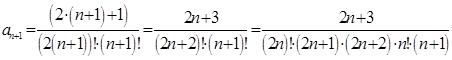 ,
, 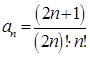
Находим m по формуле:
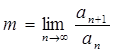
Тогда:
Следовательно, ряд
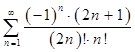 сходится абсолютно.
сходится абсолютно.
Вычисляем члены ряда с точностью до 4 цифр после запятой до тех пор, пока какой-нибудь член ряда по модулю не будет меньше α. = 0,001:
а1 = -1,5 а2 = 0,1042 а3 = - 0,0016 а4 = 0,0000093
Для приближённого вычисления ряда достаточно первых трех членов ряда (по следствию признака Лейбница: сумма сходящегося знакопеременного числового ряда не превышает его первого члена). Следовательно, ошибка при вычислении не превысит 0,0000093, а, значит, и ![]() . Требуемая точность достигнута.
. Требуемая точность достигнута.
Следовательно:
 .
.
Ответ:  .
.
8. Найти область сходимости функционального ряда
![]()
Решение.
Рассмотрим два интервала:
1) ![]()
Проверим необходимый признак сходимости рядов:![]()
Необходимый признак не выполняется. Следовательно, при ![]() ряд
ряд ![]() расходится.
расходится.
2) ![]() , то есть
, то есть ![]()
Проверим необходимый признак сходимости рядов:![]()

Необходимый признак не выполняется. Следовательно, при ![]() ряд
ряд ![]() расходится.
расходится.
При ![]() имеем:
имеем: