Контрольная работа: Управление динамической системой
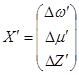
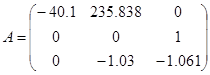
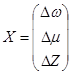(6)
С дискретным временем
, где
7 Оценка управляемости системы
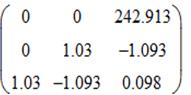Составим матрицу К:
Ранг матрицы K равен 3, что равно размерности системы (5), следовательно, система управляема.
Найдем коэффициент k0 регулятора замкнутой системы на границе устойчивости по критерию Рауса-Гурвица.
Сначала составим характеристическое уравнение для системы (6).
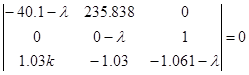
(7)
Найдем k по критерию Рауса-Гурвица.
Определитель Рауса-Гурвица составляется из коэффициентов характеристического уравнения и имеет свойство 
. где ∆n и ∆n-1 определители матрицы, an свободный член характеристического уравнения.
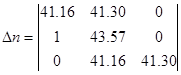
Проверим ∆1 , ∆2 :
∆1 = |41.16| = 41.16 > 0
∆2 = 
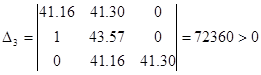
Условие границы устойчивости, если хотя бы один определитель будет равен нулю. Пусть ∆n =0, тогда аn =0. Получим:
, отсюда k0 =0.169.
8 Оценка устойчивости системы
Найдем корни характеристического уравнения (7) λ1 , λ2 , λ3 при различном Коэффициенте регулятора k, k = k0 *α = 0.169* α, где α=0.6..0.9.
Таблица 4 – Корни характеристического уравнения замкнутой системы
| α=0.6 | α=0.7 | α=0.8 | α=0.9 | |
| λ1 | -1.13 | -1.30 | -1.45 | -1.59 |
| λ2 | -2.29 | -2.47 | -2.64 | -2.79 |
| λ3 | -40.00 | -39.99 | -39.97 | -39.96 |
Построим графики изменения λ1 , λ2 , λ3 .
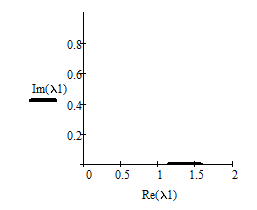
Рисунок 6 – График изменения λ1
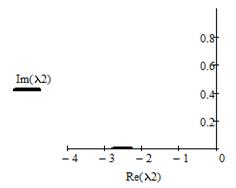
Рисунок 7 – График изменения λ2