Контрольная работа: Управление динамической системой

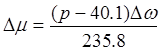
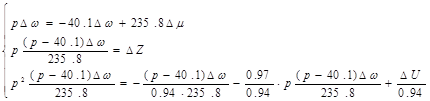
Выразим ∆ω через U:

→

получили выражение вида , где W(p) есть передаточная функция комплексной переменной, имеющая вид:

(8)

11 Амплитудная, фазовая, вещественная, мнимая и амплитудно-фазовая частотные характеристики

Подставим в передаточную функцию (8) в качестве комплексного аргумента iω, получим:

Умножим числитель и знаменатель правой части на число сопряженное знаменателю, получим и выделим действительную и мнимую части передаточной функции Re(ω) и Im(ω):

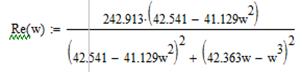
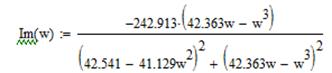
Построим графики.

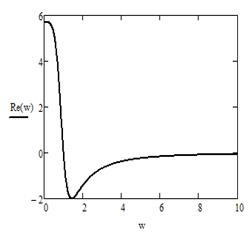
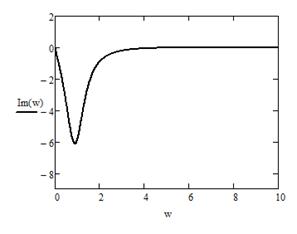
Рисунок 12 - График Re(ω)Рисунок 13 - График Im(ω)

Получим амплитудную, фазовую и амплитудно-фазовую частотные характеристики системы. Построим графики функций:

- амплитудная характеристика (рис. 14).

- фазовая характеристика (рис. 15).

Для АФХЧ отложим на графике по вертикальной оси значения мнимой части, а по горизонтальной действительной части, при ω=1..100 с шагом 0.001. Рисунок 16.

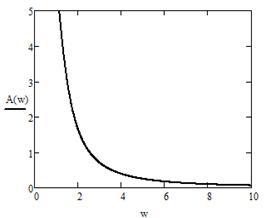
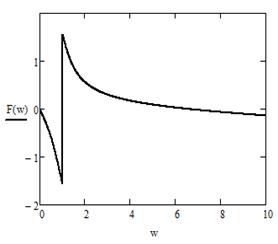
Рисунок 14 - График A(ω) Рисунок 15 - Графики Ф(ω)

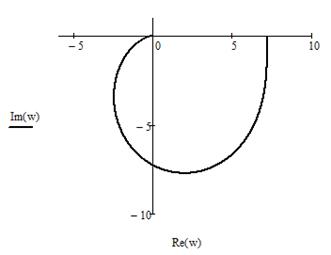
Рисунок 16 - Годограф АФЧХ

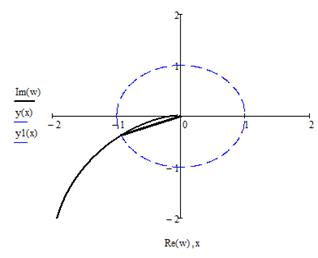
Рисунок 17 - Годограф АФЧХ

12 Оценка устойчивости системы по критерию Найквиста ,по критерию Михайлова

Оценим устойчивость системы по критерию Найквиста. Годограф АФЧХ не охватывает точку (-1,0), следовательно, система устойчива. Найдем запасы устойчивости системы по фазе и по амплитуде.