Контрольная работа: Уравнения линейной регрессии

Fтаб=5,32, т.к. k1=1, k2=8, α=0,05

т.к. F значительно больше Fтабл, то можно сделать вывод, что уравнение регрессии с вероятностью 95% статистически значимо.

Оценим точность модели на основе использования средней относительной ошибки аппроксимации.

Расчеты произведены в табл. 2.

,

значит, линейную модель можно считать точной, т.к. Е<5%/

6. С помощью линейной модели осуществим прогноз Y при α=0,1 и х=0,8хmax

Определим границы прогноза. t0,1;8=1,86

Найдем границы интервала:

7. Представим графически фактические и модельные значения Y, точки прогноза.

Рис. 2. Фактические данные, линейная модель и результаты прогнозирования.

8. а) Составим уравнение гиперболической модели. Гиперболическая модель имеет вид

;

Проведем линеаризацию переменной путем замены .

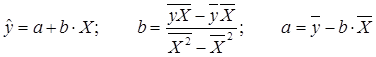
Расчеты произведем в табл. 3.

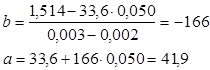
Модель имеет вид:

Табл.1.4.

t	y	x	Х	уХ
1	43	33	0,030	1,290	0,001	36,870	6,130	37,577	0,143
2	27	17	0,059	1,593	0,003	32,135	-5,135	26,368	0,190
3	32	23	0,043	1,376	0,002	34,683	-2,683	7,198	0,084
4	29	17	0,059	1,711	0,003	32,135	-3,135	9,828	0,108
5	45	36	0,028	1,260	0,001	37,289	7,711	59,460	0,171
6	35	25	0,040	1,400	0,002	35,260	-0,260	0,068	0,007
7	47	39	0,026	1,222	0,001	37,644	9,356	87,535	0,199
8	32	20	0,050	1,600	0,003	33,600	-1,600	2,560	0,050
9	22	13	0,077	1,694	0,006	29,131	-7,131	50,851	0,324
10	24	12	0,083	1,992	0,007	28,067	-4,067	16,540	0,169
∑	336	235	0,495	15,138	0,029	297,985	1,445
Средн	33,6	23,5	0,050	1,514	0,003

Найдем индекс корреляции по формуле

,
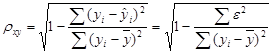