Контрольная работа: Уравнения линейной регрессии

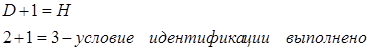
Для проверки на достаточное условие идентификации составим матрицу из коэффициентов при отсутствующих переменных.

уравнение	Отсутствующие переменные
	х3	х4
2	0	а24
3	а33	0

Составим матрицу из коэффициентов

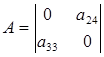
Определитель матрицы не равен 0, ранг равен 2. достаточное условие идентификации выполняется и 1-е уравнение точно идентифицируемо.

2) Во 2-м уравнении 3 эндогенные переменные y1, y2, y3 (Н=3); отсутствуют экзогенные х2, х3 (D=2).

2+1=3 — необходимое условие идентификации выполнено.

Для проверки на достаточное условие составим матрицу из коэффициентов при отсутствующих переменных.

уравнение	Отсутствующие переменные
	х2	х3
1	а12	0
3	а32	а33

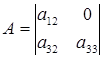
Определитель не равен 0, ранг матрицы равен 2, достаточное условие идентификации выполняется. 2-е уравнение точно идентифицируемо.

3) В 3-м уравнении 2 эндогенные переменные y2, y3 (Н=2); отсутствует 1 экзогенная х4 (D=1).

1+1=2 — необходимое условие идентификации выполняется.

Составим матрицу из коэффициентов при отсутствующих переменных.

уравнение	Отсутствующие переменные
	у1	х4
1	-1	0
3	b21	а24

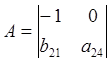
Определитель не равен 0, ранг матрицы равен 2-м, достаточное условие идентификации выполняется. 3-е уравнение точно идентифицируемо.

Т.о, если все 3 уравнения идентифицируемы, то и СФМ идентифицируема.

б) СФМ имеет вид:

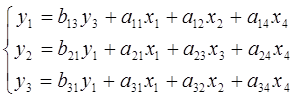
Проверим систему на идентифицируемость, для этого проверим каждое уравнение на выполнение необходимого и достаточного условия идентификации.

1) В 1-м уравнении 2 эндогенных переменных y1, y3 (Н=2); отсутствующая экзогенная переменная х3 (D=1).

Составим матрицу из коэффициентов при отсутствующих переменных.

уравнение	Отсутствующие переменные
	у2	х3
2	-1	а23
3	0	0

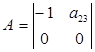
Достаточное условие не выполнено, уравнение не идентифицируемо.

2) Во 2-м уравнении 2 эндогенных переменных y1, y2 (Н=2). Отсутствующая экзогенная переменная х2 (D=1). Необходимое условие D+1=H выполняется.