Контрольная работа: Уравнения линейной регрессии
Проведем линеаризацию переменных путем логарифмирования обеих частей уравнения.
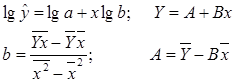
Табл. 1.6.
| t | y | x | Y | Yx |  |  |  |  |  |
| 1 | 43 | 33 | 1,633 | 53,889 | 1089 | 42,343 | 0,657 | 0,432 | 0,015 |
| 2 | 27 | 17 | 1,431 | 24,327 | 289 | 27,220 | -0,220 | 0,048 | 0,008 |
| 3 | 32 | 23 | 1,505 | 34,615 | 529 | 32,126 | -0,126 | 0,016 | 0,004 |
| 4 | 29 | 17 | 1,462 | 24,854 | 289 | 27,220 | 1,780 | 3,168 | 0,061 |
| 5 | 45 | 36 | 1,653 | 59,508 | 1296 | 46,001 | -1,001 | 1,002 | 0,022 |
| 6 | 35 | 25 | 1,544 | 38,600 | 625 | 33,950 | 1,050 | 1,102 | 0,030 |
| 7 | 47 | 39 | 1,672 | 65,208 | 1521 | 49,974 | -2,974 | 8,845 | 0,063 |
| 8 | 32 | 20 | 1,505 | 30,100 | 400 | 29,571 | 2,429 | 5,900 | 0,076 |
| 9 | 22 | 13 | 1,342 | 17,446 | 169 | 24,374 | -2,374 | 5,636 | 0,108 |
| 10 | 24 | 12 | 1,380 | 16,560 | 144 | 23,710 | 0,290 | 0,084 | 0,012 |
| ∑ | 336 | 235 | 15,127 | 365,107 | 6351 | 26,233 | 0,399 | ||
| Средн | 33,6 | 23,5 | 1,513 | 36,511 | 635,1 |
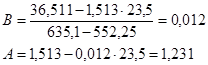
Перейдем к исходным переменным, выполнив потенцирование уравнения.
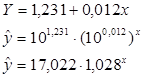
Найдем индекс корреляции.
,
значит, связь между объемом капиталовложений Х и выпуском продукции Y тесная, т.к. 
.
Индекс детерминации найдем по формуле 
. Значит, вариация объема выпуска продукции Y на 96,2% объясняется вариацией объема капиталовложений X.
Проверим значимость уравнения на основе F-критерия Фишера.
F>Fтабл (202,528>5,32),
значит, уравнение статистически значимо.
Оценим точность модели на основе средней относительной ошибки аппроксимации.
,
значит, расчетные значения ŷ для гиперболической модели отличаются от фактических значений на 3,99%. Модель точная.
9. Сравним полученные модели.
Табл. 1.7.
| Модель регрессии |  |  | F-критерий |  |
| Линейная | 0,992 | 0,984 | 492 | 3,2 |
| Гиперболическая | 0,756 | 0,572 | 10,692 | 14,45 |
| Степенная | 0,991 | 0,982 | 436,448 | 3,46 |
| Показательная | 0,981 | 0,962 | 202,528 | 3,99 |
Наилучшей моделью является линейная модель 
(по максимуму критерия корреляции, детерминации, F-критерия и минимальной средней ошибке аппроксимации).
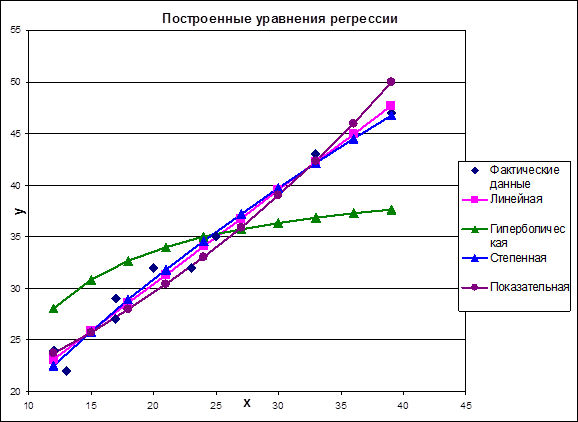
Рис. 3. Построенные уравнения регрессии.
Задача 2 (а, б)
Для каждого варианта даны по две СФМ, которые записаны в виде матриц коэффициентов модели. Необходимо записать системы одновременных уравнений и проверить обе системы на идентифицируемость.
Табл. 2.1.
| Номер варианта | Номер уравнения | Задача 2а | Задача 2б | ||||||||||||
| переменные | переменные | ||||||||||||||
| y1 | y2 | y3 | x1 | x2 | x3 | x4 | y1 | y2 | y3 | x1 | x2 | x3 | x4 | ||
| 6 | 1 | -1 | b12 | b13 | a11 | a12 | 0 | 0 | -1 | 0 | b13 | a11 | a12 | 0 | a14 |
| 2 | b21 | -1 | b23 | a21 | 0 | 0 | a24 | b21 | -1 | 0 | a21 | 0 | a23 | a24 | |
| 3 | 0 | b32 | -1 | a31 | a32 | a33 | 0 | b31 | 0 | -1 | a31 | a32 | 0 | a34 | |
Решение
a) CФМ имеет вид:
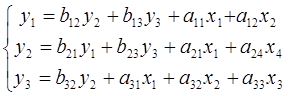
Проверим систему на идентифицируемость. Для этого проверим каждое уравнение системы на выполнение необходимого и достаточного условия идентификации.