Курсовая работа: Анализ методов определения минимального, максимального значения функции при наличии ограничений

Работа алгоритма симплексного поиска начинается с построения регулярного симплекса в пространстве независимых переменных и оценивания значений целевой функции в каждой из вершин симплекса. При этом отбрасывается вершина, которой соответствует наибольшее значение целевой функции.

Преимущества метода:

· сравнительная простота логической структуры метода и, соответственно, программы для ЭВМ;

· используется сравнительно небольшое число заранее установленных параметров;

· невысокий уровень требований к ЭВМ;

· алгоритм эффективен даже в тех случаях, когда ошибка вычисления значений целевой функции велика, т.к. при его реализации используют наибольшие значения функции в вершинах, а не меньшие.

Недостатки метода:

· возникает проблема масштабирования, поскольку все координаты вершин симплекса зависят от одного масштабного множителя. Чтобы избежать такого рода проблем в практических задачах, следует промасштабировать все переменные с тем, чтобы их значения были сравнимы по величине;

· алгоритм работает достаточно медленно, т.к. полученная на предыдущих итерациях информация не используется для ускорения поиска;

· не существует простого способа расширения симплекса. Требуется перерасчет значений целевой функции во всех точках образца.

Градиентные методы

Важность прямых методов неоспорима, т.к. в практических задачах информация о значениях целевой функции является единственно надежной информацией, которой располагает инженер. Однако, если существует и непрерывны целевая функция f(x) и ее первые производные, aтакже они могут быть записаны в аналитическом виде (или с достаточно высокой точностью вычислены при помощи численных методов), то целесообразно использовать методы, основанные на использовании градиента целевой функции.

Градиент функции F(x) – это вектор, составляющие которого равны частным производным функции F(x) по соответствующим переменным, т.е.

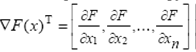
Направление вектора градиента совпадает с направлением наискорейшего возрастания функции. Вектор противоположного знака -ÑF(x) называется антиградиентом, его направление совпадает с направлением наискорейшего убывания функции.

Матрица вторых производных Ñ2F(x) – это симметричная квадратная матрица порядка n вторых частных производных функции F(x). Эту матрицу называют матрицей Гессе и обозначают H(x) = Ñ2F(x). Ее элемент, расположенный на пересечении i-й строки и j-го столбца, равен:

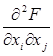
Пусть х^Т =[x₁ , x₂ ,…, x_n ] – вектор переменных. Для наличия в точке x* локального минимума (максимума) необходимо, чтобы выполнялось равенство ÑF(x*) =0 и матрица Гессе H(x*) = Ѳ F(x*) была положительно (отрицательно) полуопределенной, т.е. x^T Hx ³0 ( x^T Hx £0).

Достаточным условием существования минимума (максимума) в точке x* является положительная (отрицательная) определённость матрицы Гессе в этой точке, т.е. x^T Hx >0 ( x^T Hx<0).

Все методы основаны на итерационной процедуре, реализуемой в соответствии с формулой x^{k +1} = x^k + a^k s(x^k ), где

x^k - текущее приближение к решению x^* ;

a^k - параметр, характеризующий длину шага;

s(x^k ) - направление поиска в N - мерном пространстве управляемых переменных x_i , i = 1, 2,..., N.

Способ определения a^k и s(x^k ) на каждой итерации связан с особенностями применяемого метода. Обычно выбор a^k осуществляется путем решения задачи минимизации f(x) в направлении s(x^k ). Поэтому при реализации градиентных методов необходимо использовать эффективные алгоритмы одномерной минимизации.

Простейший градиентный метод

В основе метода лежит следующая итерационная модификация формулы

x^{k +1} = x^k + a^k s(x^k ),

x^k+1 = x^k - a^k Ñf(x^k ), где

a - заданный положительный коэффициент;

Ñf(x^k ) - градиент целевой функции первого порядка.

Недостатки: