Курсовая работа: Анализ методов определения минимального, максимального значения функции при наличии ограничений

j (a)=f (x^{( k )} -aÑf (x^{( k )} ))

Воспользуемся для этого методом золотого сечения.

Алгоритм метода наискорейшего спуска состоит в следующем.

1. Задаются координаты начальной точки x⁽⁰⁾ .

2. В точке x^{( k )} , k = 0, 1, 2, …, вычисляется значение градиентаÑf (x^{( k )} ).

3. Определяется величина шага a_k путем одномерной минимизации по a функции

j (a)=f (x^{( k )} -aÑf (x^{( k )} )).

4. Определяются координаты точки x^{( k )} :

x_i ^(k+1) = x_i ^(k) -a_k Ñf_i (x^(k) ), i=1, …, n.

5. Проверяется условие останова итерационного процесса:

||Ñf (x^{( k +1)} )||£e .

Если оно выполняется, то вычисления прекращаются. В противном случае осуществляется переход к п. 1. Геометрическая интерпретация метода наискорейшего спуска представлена на рис. 1.

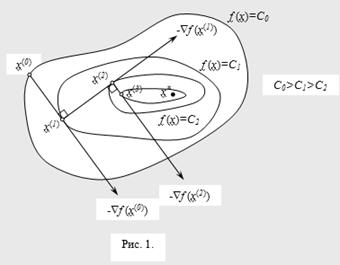
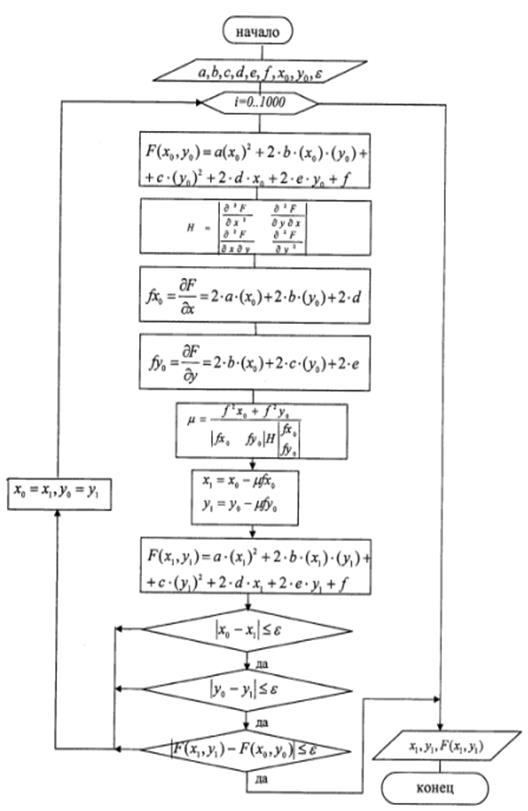
Рис. 2.1. Блок схема метода наискорейшего спуска.

Реализация метода в программе:

Метод наискорейшего спуска.

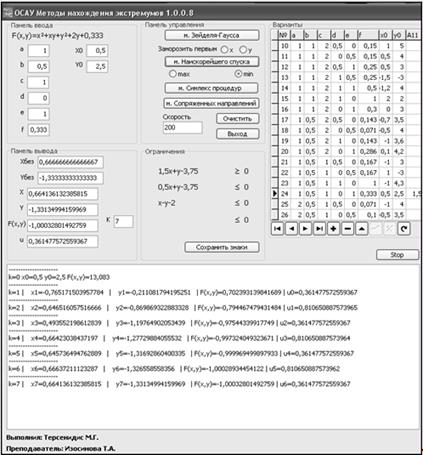
Рис. 2.2. Реализация метода наискорейшего спуска.

Вывод: В нашем случае метод сошёлся за 7 итераций. Точка А7 (0,6641; -1,3313) является точкой экстремума. Метод сопряженных направлений. Для квадратичных функций можно создать градиентный метод, при котором время сходимости будет конечным и равно числу переменных n.

Назовем некоторое направление и сопряженными по отношению к некоторой положительно определенной матрице Гесса H, если выполняется:

Если ,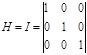

Тогда т.е. . Значит при единичной H, сопряженное направление означает их перпендикуляр. В общем же случае Hнеединичная. В общем случае сопряженность - это применение матрицы Гесса к вектору - означает поворот этого вектора на некоторый угол и его растяжение или сжатие.

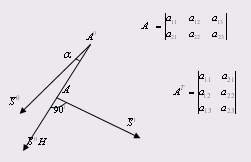
А теперь вектору вектор ортогонален т. е. сопряженность это не ортогональность векторов и , а ортогональность повернутого вектора т.е. и .

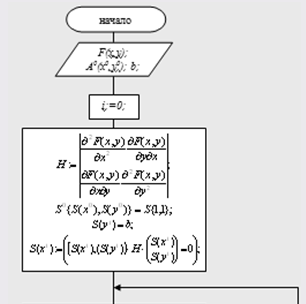
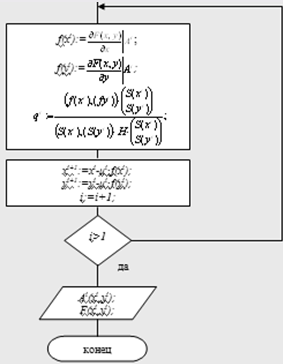
Рис. 2.3. Блок-схема метода сопряженных направлений.

Реализация метода в программе: Метод сопряженных направлений.

Рис. 2.4. Реализация метода сопряженных направлений.