Рис. 2.5. График метода сопряженных направлений.

Вывод: Точка А3 (0,6666; -1,3333), была найдена за 3 итерации и является точкой экстремума.

3. Анализ методов определения минимального, максимального значения функции при наличии ограничений

Напомним, что общая задача условной оптимизации выглядит так

f(x) ® min, x Î W,

где W — собственное подмножество R^m . Подкласс задач с ограничениями типа равенств выделяется тем, что множество  задается ограничениями вида

f_i (x) = 0, гдеf_i : R^m ®R (i = 1, …, k).

Таким образом,W = {x Î R^m : f_i (x) = 0, i = 1, …, k}.

Нам будет удобно писать у функции f индекс "0". Таким образом, задача оптимизации с ограничениями типа равенств записывается в виде

f₀ (x) ® min, (3.1)

f_i (x) = 0, i = 1, …, k. (3.2)

Если обозначить теперь через f функцию на R^m со значениями в R^k , координатная запись которой имеет вид f(x) = (f₁ (x), …, f_k (x)), то (3.1)–(3.2) можно также записать в виде

f₀ (x) ® min, f(x) = Q.

Геометрически задача с ограничениями типа равенств — это задача о поиске наинизшей точки графика функции f₀ над многообразием  (см. рис. 3.1).

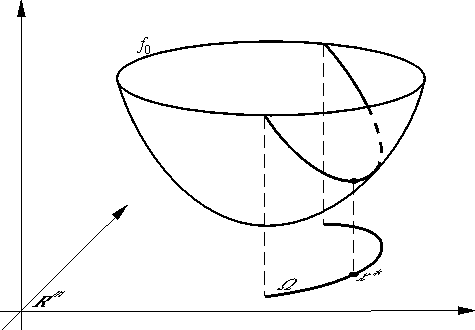
Рис. 3.1.

Точки, удовлетворяющие всем ограничениям (т. е. точки множества ), обычно называют допустимыми . Допустимая точка x* называется условным минимумом функции f₀ при ограничениях f_i (x) = 0, i = 1, ..., k (или решением задачи (3.1)–(3.2)), если при всех допустимых точках x f₀ (x*)  f₀ (x). (3.3)

Если (3.3) выполняется только для допустимых x, лежащих в некоторой окрестности V_x* точки x*, то говорят о локальном условном минимуме . Естественным образом определяются понятия условных строгих локального и глобального минимумов .

Правило множителей Лагранжа

Описываемый ниже необходимый признак локального условного минимума был сформулирован Лагранжем. Определим F: R^m ® R^k+1 , положив F(x) = (f₀ (x), f₁ (x), ..., f_k (x)). Заданная на R^m ×R^k+1 скалярная функция Лагранжа M по определению принимает значения в R и задается равенством

M(x, m) = (m, F(x)) = m_i f_i (x) (xÎR^m , m ÎR^{k +1} ).

Координаты вектора m, т. е. числа m₀ , m₁ , ..., m_k называются множителями Лагранжа или двойственными переменными . Оказывается, имеет место следующая теорема, часто именуемая правилом множителей Лагранжа :

Теорема. Пусть F Î C¹ и x* — локальный условный минимум функции f₀ при ограничениях f_i (x) = 0 (i = 1, ..., k). Тогда найдется ненулевой вектор m* такой, что x* является стационарной точкой функции x M(x, *):

M¢_x (x, m*)|_{x = x *} =m*_i f¢_i (x*)= Q.

Правило множителей Лагранжа доставляет необходимое условие локального условного минимума и поэтому позволяет искать точки, "подозрительные" на экстремум. В самом деле, для нахождения точки (x*, m*) Î R^m+k+1 , т. е. для нахождения m + k + 1 неизвестных, мы имеем m + k уравнений

f(x) = Q, M¢_x (x, l)= Q.

Поскольку, очевидно, множители Лагранжа можно искать с точностью до постоянного множителя, то в общей ситуации этих уравнений хватает для отыскания x*.

Регулярные точки

Допустимая точка x задачи (3.1)–(3.2) называется регулярной , если векторы {f _i (x)}^k _i=1 линейно независимы. Оказывается, что если x* — регулярная точка минимума, то в векторе * можно считать *₀ ненулевым, а поскольку множители Лагранжа определяются с точностью до множителя, можно считать, что *₀ = 1. Чтобы сформулировать это утверждение более точно, введем следующие обозначения. Пусть   R^k , а функция Лагранжа в регулярном случае определяется равенством

L(x, l) = f₀ (x) + (l, f(x)) = f₀ (x) +l_i f_i (x) (x Î R^m , l Î R^k ).

Очевидно, L(x, l) = M(x, m),  m = (1, l).