Курсовая работа: Анализ нагруженности плоского рычажного механизма
(1.2.38);
Полученные данные сведем в таблицу.
| Aa м/с 2 |  , м/с 2 |  , м/с 2 | aC , м/с 2 |  , м/с 2 |  , м/с 2 |  , м/с 2 |  |  | aF , м/с 2 |
| 153.8 | 23.12 | 18 | 90 | 42.6 | 85.5 | 108 | 23.18 | 18.9 | 36 |
 , м/с 2 |  , м/с 2 | aS3 , м/с 2 | aS4 , м/с 2 | aS5 , м/с 2 |
| 85.5 | 110.7 | 45 | 98.1 | 20 |
Таблица 1.2.3 – Ускорения точек и центров масс звеньев
Определение угловых ускорений звеньев механизма.
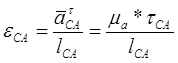(1.2.39);
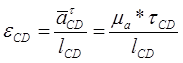(1.2.40);
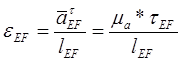(1.2.41);
Угловые ускорения звеньев сведем в таблицу
 , |  , |  , |  , |
| 0 | 225 | 1710 | 180 |
Таблица 1.2.4. – Угловые ускорения звеньев.
1.3 КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА
Кинетостатический расчет, положенный в основу силового расчета механизма, базируется на принципе Д’Аламбера, который в общем случае движения звеньев механизмов, совершающих сложное плоское движение, позволяет решить задачу путем сведения сил инерции звеньев к главному вектору инерции Fi и к главному моменту сил Mi .
(1.3.1)
Знак “-” означает, что вектор силы инерции направлен в сторону противоположную ускорению центра масс.
Массы звеньев рассчитываются с помощью формулы:
(1.3.2)
где q = 0.1 кг/м,
l – длина звена.
m = P/g,
где P – вес звена (H),
g – ускорение свободного падения.
g = 9.8 м/с2 .
Также существует главный момент инерции звена, который приложен к центру масс звена и направлен в противоположную угловому ускорению звена сторону
(1.3.3)
где 
— момент инерции звена,