Курсовая работа: Анализ рядов распределения

,

взвешенная дисперсия

.

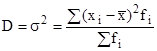Формулу для расчета дисперсии можно упростить:

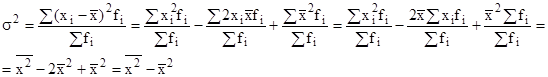
Таким образом, дисперсия равна разности средней из квадратов вариант и квадрата средней из вариант совокупности:

.

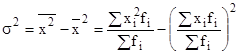Однако, вследствие суммирования квадратов отклонений дисперсия дает искаженное представление об отклонениях, поэтому ее на основе рассчитывают среднее квадратическое отклонение, которое показывает, на сколько в среднем отклоняются конкретные варианты признака от их среднего значения. Вычисляется путем извлечения квадратного корня из дисперсии:

для несгруппированных данных

,

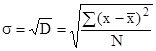для вариационного ряда

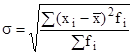
Чем меньше значение дисперсии и среднего квадратического отклонения, тем однороднее совокупность, тем более надежной (типичной) будет средняя величина.

Среднее линейное и среднее квадратичное отклонение - именованные числа, т.е. выражаются в единицах измерения признака, идентичны по содержанию и близки по значению. Рассчитывать абсолютные показатели вариации рекомендуется с помощью таблиц.

Таблица 3 - Расчет характеристик вариации (на примере срока данных о сменной выработке рабочих бригады)

Группы рабочих по выработке, шт.	Число рабочих,	Середина интервала,	Расчетные значения
170-190	10	180	1800	-36	360	1296	12960
190-210	20	200	4000	-16	320	256	5120
210-230	50	220	11000	4	200	16	800
230-250	20	240	4800	24	480	576	11520
Итого:	100	-	21600	-	1360	-	30400

Среднесменная выработка рабочих:

Среднее линейное отклонение:

Дисперсия выработки:

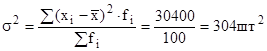
Среднее квадратическое отклонение выработки отдельных рабочих от средней выработки:

.

2.1.1 Расчет дисперсии способом моментов

Вычисление дисперсий связано с громоздкими расчетами (особенно если средняя величина выражена большим числом с несколькими десятичными знаками). Расчеты можно упростить, если использовать упрощенную формулу и свойства дисперсии.

Дисперсия обладает следующими свойствами:

если все значения признака уменьшить или увеличить на одну и ту же величину А, то дисперсия от этого не уменьшится:

,

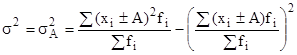если все значения признака уменьшить или увеличить в одно и то же число раз (hраз), то дисперсия соответственно уменьшится или увеличится в раз.

То есть, если дисперсию уменьшенных значений признака описать следующим выражением