Курсовая работа: Анализ рядов распределения

Используя свойства дисперсии и сначала уменьшив все варианты совокупности на величину А, а затем разделив на величину интервала h, получим формулу вычисления дисперсии в вариационных рядах с равными интервалами способом моментов:

,

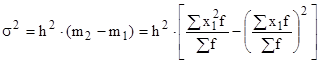где - дисперсия, исчисленная по способу моментов;

h- величина интервала вариационного ряда;

- новые (преобразованные) значения вариант;

А- постоянная величина, в качестве которой используют середину интервала, обладающего наибольшей частотой; либо вариант, имеющий наибольшую частоту;

- квадрат момента первого порядка;

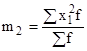- момент второго порядка.

Выполним расчет дисперсии способом моментов на основе данных о сменной выработке рабочих бригады.

Таблица 4 - Расчет дисперсии по способу моментов

Группы рабочих по выработке, шт.	Число рабочих,	Середина интервала,	Расчетные значения
170-190	10	180	-2	-20	40
190-210	20	200	-1	-20	20
210-230	50	220	0	0	0
230-250	20	240	1	20	20
Итого	100	-	-	-20	80

Порядок расчета:

определяем постоянное число А, это варианта с наибольшей частотой: А=220;

определяем ;

рассчитываем и ;

определяем моменты 1-го и 2-го порядка:

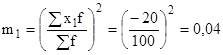
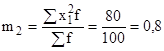
рассчитываем дисперсию:

2.1.2 Расчет дисперсии альтернативного признака

Среди признаков, изучаемых статистикой, есть и такие, которым свойственны лишь два взаимно исключающих значения.

Это альтернативные признаки.

Им придается соответственно два количественных значения: варианты 1 и 0.

Частостью варианты 1, которая обозначается p, является доля единиц, обладающих данным признаком. Разность 1-р=q является частостью варианты 0. Таким образом,

хi	wi
1	p
0	q

Средняя арифметическая альтернативного признака

, т.кp+q=1.

Дисперсия альтернативного признака

, т.к1-р=q

Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком, и доли единиц, не обладающих этим признаком.

Если значения 1 и 0 встречаются одинаково часто, т.е. p=q, дисперсия достигает своего максимума pq=0,25.