Курсовая работа: Аналіз типової системи автоматичного регулювання температури в печі
;
;
Диференціальне рівняння руху системи за каналом завдання-вихід матиме вигляд:
/3.5/
А відповідне рівняння статики:
/3.6/
З виразу /3.4/ знаходимо операторну форму диференційного рівняння, яке описує рух системи за каналом збурення-вихід:
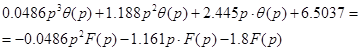
Виконавши обернене перетворення Лапласа, одержимо:
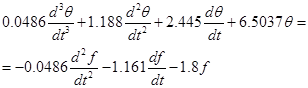/3.7/
Рівняння статики системи за каналом збурення:
/3.8/
5. Аналіз стійкості системи та визначення критичного значення коефіцієнта передачі регулятора
При розробці і настроюванні систем автоматичного керування важливо встановити вплив окремих параметрів на їх стійкість. Для визначення областей допустимих значень параметрів можуть бути використані критерії стійкості та загальний метод D-розбиття.
Зокрема, критичне значення параметру (коефіцієнта передачі 
чи постійної часу 
) при якому система знаходиться на межі області стійкості можна визначити за критерієм Гурвіца. [2, c.131]
Запишемо характеристичне рівняння системи, передаточна функція якої /3.3/:
/4.1/
Складемо визначник Гурвіца для даного рівняння:
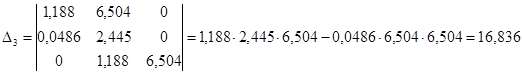/4.2/
;
Головний визначник Гурвіца 
>0 і його мінори 
>0, 
>0, тому система з даними параметрами стійка.
Визначення критичного значення коефіцієнта передачі регулятора
Критичне значення коефіцієнта передачі підсилювача знайдемо, прийнявши його за невідомий у виразі /3.2/ та прирівнявши до нуля визначник Гурвіца:
;
/4.3/
Характеристичне рівняння замкнутої системи
/4.4/
Складемо мінор другого порядку визначника Гурвіца, оскільки він однозначно залежить від значення визначника Гурвіца (
):
