Курсовая работа: Аналіз типової системи автоматичного регулювання температури в печі

В результаті сума доданків, що відповідають парі комплексно-спряжених коренів може бути зведена, з врахуванням формули Ейлера, до одного виразу:

/6.5/

Тоді вираз перехідної функції матиме вигляд

/6.6/

де - дійсний корінь характеристичного рівняння /6.2/; - похідна від полінома знаменника передаточної функції; і - відповідно дійсна та уявнf частини пари комплексних чисел , , α і ω - відповідно дійсна та уявна частини пари комплексно-спряжених коренів p₂ ,p_3.

M (p) =5.5037;

D (p ) =;

;

Підрахуємо:

; /6.7/

; /6.8/

Відповідно

. /6.9/

=0,4813;

=2,622;

.

Підставивши у /6.6/, отримаємо рівняння перехідної характеристики:

/6.10/

Для графічної побудови перехідної характеристики обчислимо значення h (t) в точках:

t	0	0,2	0,4	0,6	0,8	1	1,5	2
h (t)	-0,00036	0,057818	0,242	0,482572	0,714802	0,896603	1,054382	0,938921

t	2,5	3	3,5	4	4,5	5
h (t)	0,818175	0,79644	0,829785	0,855775	0,857287	0,848411

t	5,5	6	6,5	7
h (t)	0,843086	0,843538	0,845765	0,846792

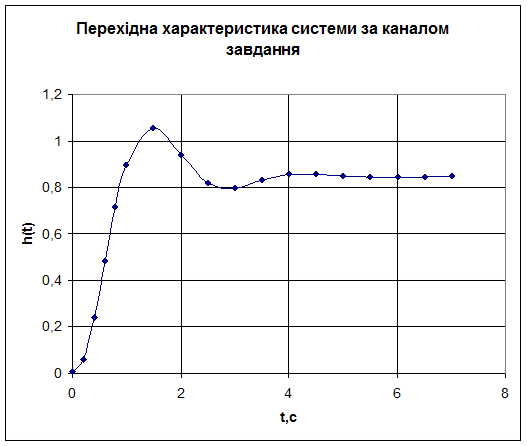
Рис.7. Перехідна характеристика системи за каналом завдання

8. Моделювання перехідних процесів за допомогою комп’ютерної програми SIAM

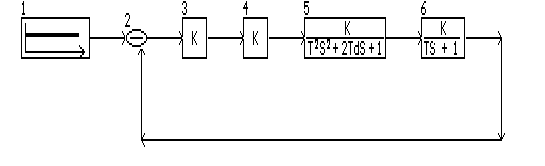
Рис. 8. Схема моделювання перехідних процесів системи автоматичного регулювання температури в печі у програмі SIAM.

Для моделювання перехідних процесів у системі автоматичного регулювання була побудована схема (рис.8), у якій задані наступні параметри моделі:

Задані параметри ланок:

K=1

K=0.84