Курсовая работа: Дифференциальное исчисление
III в.: f(x) = 4 – x3
IVв.: f(x) = 5x4 + 2x3 – 3x + 6
5. Найдите производную функций в данных точках.
I в.: f(x) = cosx, при х = 
II в.: f(x) = tgx, при х = 
III в.: f(x) =cos 2x, при х = 
IVв.: f(x) = x2 + 4x + 72, при х = -5
Приложение 3
Конспект урока на тему "Производная"
1. Задачи, приводящие к понятию производной.
Рассмотрим движение материальной точки М вдоль оси Ох (рис.1). За начало отсчета (точка О) примем положение материальной точки в момент времени t = 0. Пусть в момент времени t координата движущейся точки х равна f(t), т.е. координата х материальной точки есть функция времени:
Х = f(t), t Є [0; T]
О М х
Эта функция называется законом движения, задается формулой:
X = Vt
На практике поезда, автомобили движутся равномерно и прямолинейно лишь на некоторых участках, а в общем случае их движение неравномерное. При неравномерном прямолинейном движении материальная точка за разные, но равные по длительности промежутки времени может совершать разные как по времени, так и по направлению перемещения. Для неравномерного движения вводится понятие средней скорости Vср , которая зависит от выбора моментов времени t0 и t1 :
Vср (t1 , t0 ) = 
Проиллюстрируем сказанное примером. Из курса физики известно, что свободное падение тел в поле тяжести Земли является неравномерным движением и совершается по закону х = 
, где g – ускорение свободного падения. Его средняя скорость за первую секунду движения, т.е. за промежуток времени от момента t0 = 0 до момента времени t1 = 1, равна:
Vср (1, 0) = 
,
в то время как для второй секунды движения (t1 = 2, t0 = 1) она уже равна в три раза большему значению:
Vср (2, 1) =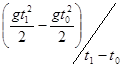 
= 
Средняя скорость не может полностью характеризовать неравномерное движение. Для полной характеристики вводят так называемую мгновенную скорость. Очевидно, что средняя скорость Vср (t1 , t0 ) тем полнее характеризует движение за промежуток времени от t0 до t1 , чем меньше длительность этого промежутка. Предел средней скорости за промежуток времени от t0 до t1 при t1 , стремящимся к t0 , называется мгновенной скоростью V(t0 ) в момент времени t0 , т.е.:
|
|
|
|