Курсовая работа: Дифференциальное исчисление
ЛИСТ
5
|
|
|
|
|
2. Производная функции
В рассмотренных выше задачах различные физические величины вводились с помощью некоторого предела одного и того же вида. Поэтому имеет смысл рассмотреть предел для функции в общем случае.
Определение. Пусть задана функция f(x), x Є(a; b), и пусть х0 – некоторая точка интервала (a; b). Предел 
называется производной функции f(x) в точке x0 и обозначается f ′ (x0 ). Таким образом, по определению:
f ′ (x0 ) =
Функция, имеющая производную в некоторой точке, называется дифференцируемой на этом интервале. Операция нахождения производной данной функции называется дифференцированием и обозначается с помощью штриха.
Если ввести приращение аргумента 
х = х – х0 и приращение функции f = f(x) – f(x0 ) = f(x0 + x) – f(x0 ), то производная функции f(x) в точке x0 запишется в виде:
f ′ (x0 ) = 
Часто для обозначения производной вместо штриха используется символ 
.
Так как х0 – произвольное значение аргумента, то будем обозначать его просто Х. Тогда:
f ′ (x) = 
Возвращаясь к рассмотренным выше задачам, можем теперь сказать, что искомые величина мгновенной скорости движения V(t) является производной от соответствующей функции:
V(t) = x ′ (t)
3 . Физический и геометрический смысл производной.
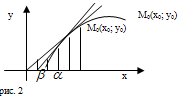
Дадим геометрическое истолкование производной. Пусть кривая К является графиком непрерывной функции у = f(x), x Є [a; b] (рис. 2). На кривой К рассмотрим точки М0 (х0 ; у0 ) и М1 (х1 ; у1 ) и проведем секущую М0 М1 . Ее угловой коэффициент k = tg
равен:
Пусть теперь 
, т.е. абсцисса точки М1 стремиться к абсциссе точки М0 , оставаясь на кривой К. При этом секущая М0 М1 , вообще говоря, меняет свое положение, вращаясь вокруг точки М0 , т.е. изменяет угол .
) Если функция f(x) дифференцируема в точке х0 , то существует предел:
= 
и следовательно, существует прямая М0 Т, являющаяся предельным положением секущей при приближении точки М1 по кривой к М0 . Эта прямая называется касательной к кривой К в точке М0 .