Курсовая работа: Динамические системы в плоской области

определено при значении t - t₀ . Пусть — два произвольных числа, причем < t₀ , > t₀ . Обозначим через конечную цилиндрическую область пространства , состоящую из всех точек М (t, x, у) таких, что , а х, у таковы, что точка (х, у) (рис. 1). Интегральная кривая, соответствующая решению (1), проходит через точку М₀ (t₀ ,,), принадлежащую области H₁ . Но тогда, в силу теоремы (А') дополнения, эта интегральная кривая выходит из области как при значении, большем t₀ , так и при значении, меньшем t₀ . Однако выйти из цилиндрической области через боковую поверхность этой области интегральная кривая не может, так как в этом случае, очевидно, нашлась бы точка N (), лежащая вне замкнутой области , что противоречит условию теоремы.

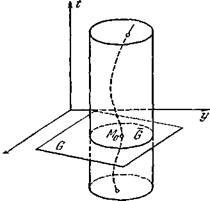
Рис. 1.

Следовательно, рассматриваемая интегральная кривая выходит из через нижнее и верхнее основания (рис. 1). Но это значит, что решение (1) определено при t= и t =. Так как произвольны, то решение (1) определено при всех значениях t. Теорема доказана.

3. Простейшие свойства решений системы (I)

Мы установим некоторые cвойства решений системы (I), являющиеся следствием автономности этой системы.

Лемма 1. Если

есть решение системы (I), определенное на интервале (, Т), то

(2)

где С — любая постоянная, также есть решение системы (I) и это решение определено на интервале ( — С, Т — С).

Доказательство. Так как (1) есть решение системы (I), то при всех t (, Т) имеет место тождественное равенство

(),.

Если заменить в этих равенствах tна t+C, то при всех t ( —С,Т — С) мы будем иметь тождественное равенство

(3)

Но, очевидно

,

и, следовательно, равенства (3) могут быть записаны в виде

Последние равенства показывают, что функции (2) являются решением системы (I). Тот факт, что это решение определено на интервале ( — С, Т — С), устанавливается простым рассуждением, которое мы опускаем. Лемма доказана.

С точки зрения геометрической интерпретации в трехмерном пространстве утверждение леммы 1 означает, что линия, получающаяся из любой интегральной кривой путем сдвига ее вдоль оси tна любой отрезок, также есть интегральная кривая. В самом деле, интегральная кривая

получается из интегральной кривой

сдвигом вдоль оси tна величину С.

Лемма 2.

а) Решения системы (I)

(1)