Курсовая работа: Динамические системы в плоской области

Ψ (t— t₀ ,0, х₀ ,у₀ )= ψ(t—t₀ , х₀ , у₀ )

устанавливает справедливость утверждения леммы.

В дальнейшем решение системы (I), соответствующее начальным значениям t₀ , х₀ , у₀ , мы всегда будем записывать в виде (6).

Лемма 4. Если решение

x = (t—t₀ , х₀ , у₀ ), y= ψ(t—t₀ , х₀ , у₀ ).(8)

определено при значении t= t₁ , и

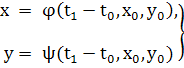(9) то

(t—t₀ , х₀ , у₀ ) (t—t₁ , х₀ , у₀ )

ψ(t—t₀ , х₀ , у₀ ) (t—t₁ , х₀ , у₀ ) (10)

Доказательство. Из соотношений (9), очевидно, следует, что решение (8) и решение

x= (t—t₁ , х₀ , у₀ ), y= (t—t₁ , х₀ , у₀ )

являются решениями, соответствующими одним и тем же начальным значениям t₁ , х₁ , y₁ . Но тогда эти решения совпадают, т. е. имеют место равенства (10).

Замечание. Полагая в тождествах (10) t = t₀ , мы получим

x₀ = (t₀ t₁ , х₁ , у₁ ) , y₀ = ψ(t₀ t₁ , х₁ , у₁ )

Это, очевидно, справедливо при любых t₁ , х₁ , у₁ удовлетворяющих соотношениям (10). Опуская индексы, мы получаем

x₀ = (t₀ —t, х, у) , y₀ = ψ(t₀ —t, х, у).

Лемма 5. Если система (I) является системой класса С_n , тoфункции

x₀ =(t—t₀ , х₀ , у₀ ) , y₀ = ψ (t—t₀ , х₀ , у₀ )

при всех значениях, входящих в них переменных, при которых эти функции определены, имеют непрерывные (по совокупности всех переменных) частные производные:

1) по t (или t₀ ) до порядка n+1 включительно,

2) по х₀ и у₀ до порядка nвключительно

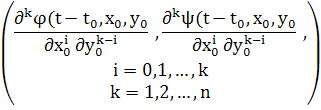
3). пot(или t₀ ) и по х₀ и у₀ —содержащие по крайней мере одно дифференцирование по t (или t₀ )—до порядка n + 1

4. Геометрическая интерпретация динамической системы на фазовой плоскости (х, у)

Геометрическая интерпретация системы (I) в трехмерном пространстве (х, у, t) в настоящей книге является вспомогательной. Основная геометрическая интерпретация автономной системы (1)связана с рассмотрением плоскости (х, у). Эта плоскость называется фазовой плоскостью системы (I).

Будем в каждой точке М (х, у) области Gплоскости (х, у) рассматривать вектор vс компонентами Р (х, у), Q(x, у). Динамическая система (I) определяет, таким образом, в области G векторное поле *).

В силу того, что Р (х, у) и Q (х, у) по предположению имеют непрерывные частные производные, векторное поле, определяемое системой (I), является так называемым непрерывно дифференцируемым векторным полем.

Пусть в точке М (х, у) хотя бы одна из величин Р (х, у), Q (х, у) не обращается в нуль. Тогда длина вектора в этой точке