Курсовая работа: Динамика плоских шарнирных механизмов
Плоский шарнирный механизм (рис. 1), расположенный в вертикальной плоскости, движется под действием внешнего момента
, приложенного к ведущему звену (кривошипу ОА) и изменяющемуся по закону
. На звено О1 D действует полезная нагрузка MH , величина которой задается соотношением
Звенья механизма моделируются сплошными однородными стержнями, массы которых пропорциональны их длине. Погонная плотность каждого стержня равна ρ. Соединение стержней осуществлено идеальными шарнирами. Движение механизма начинается из состояния покоя, а начальное значение угла поворота ведущего звена равно φ = 0.
Требуется
- Составить дифференциальное уравнение движения механизма с помощью
теоремы об изменении кинетической энергии.
- Определить динамические реакции внешних и внутренних связей.
- Провести численное интегрирование дифференциального уравнения движения при заданных начальных условиях с помощью пакета Mathcad.
- Провести анализ результатов вычислений.
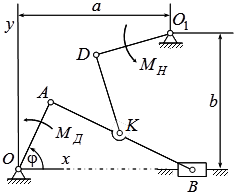
Рис. 1 Схема механизма
Дано:
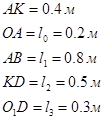
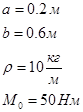
2. Составление дифференциального уравнения движения механизма
Для решения поставленной задачи выберем правую систему координат, начало которой расположим в подшипнике О. Рассмотрим механизм в произвольном положении и изобразим силы, действующие на него в данный момент времени (рис.2): 
- силы тяжести звеньев; MH - полезная нагрузка; МД - возмущающий момент; 
- реакции опор.
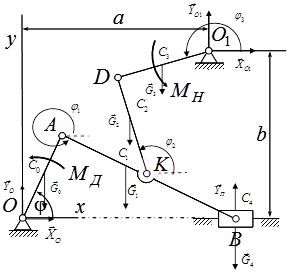
Рис.2 Расчётная схема механизма.
2.1 Составление кинематических соотношений
Рассматриваемый механизм представляет собой механическую систему с одной степенью свободы. Положение всех его звеньев будем определять с помощью угла поворота ведущего звена φ. Углы поворотов звеньев φk (k=1,2,3), отсчитываются от горизонтальной оси Ох в положительном направлении.
Выразим кинематические характеристики всех тел механизма через кинематические параметры ведущего звена с помощью уравнений геометрических связей (подробное описание этой процедуры можно получить в КР по кинематике 21 вариант за 2006 г.)
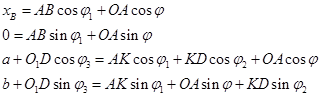(1)
Угловые координаты звеньев механизма и координата ползуна B будут определяться соотношениями
(2)
где - 
Угловые скорости звеньев можно получить из соотношения