Курсовая работа: Динамика плоских шарнирных механизмов

Шатун АB:

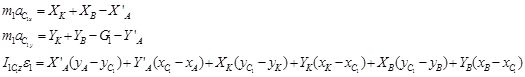(19)

Шатун KD:

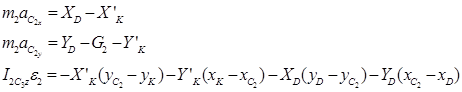(20)

Кривошип О₁ D:

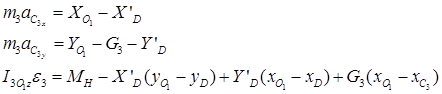(21)

Ползун B:

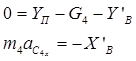(22)

Первое уравнение системы (22) позволяет определить реакцию опорной плоскости Y_П , а третье из системы (18), после подстановки найденных величин, дифференциальное уравнение движения механизма (17).

Оставшиеся двенадцать соотношений представляют собой систему линейных алгебраических уравнений относительно неизвестных реакций.

4. Результаты расчетов

Решение поставленной задачи сводится к численному интегрированию дифференциального уравнения движения механизма (17) и решению системы двенадцати линейных алгебраических уравнений (18) - (21) относительно неизвестных динамических реакций внешних и внутренних связей.

Задача интегрирования дифференциального уравнения (17) связана с большим количеством предварительных вычислений и может быть условно разбита на пять блоков:

о решение системы уравнений геометрических связей (1) или вычисление геометрических соотношений (2);

о вычисление кинематических соотношений по формулам (3) - (11);

о вычисление приведенного момента инерции механизма и приведенного момента внешних сил.

о вычисление производной от приведенного момента инерции по углу поворота ведущего звена.

о численное интегрирование дифференциального уравнения.

Все это может быть проведено в Mathcad несколькими способами использующими различные встроенные процедуры-функции. Отличие этих способов и методов заключается во времени вычислений, которое требуется для нахождения: решения системы уравнений геометрических связей, приведенного момента инерции механизма и его производной, приведенного момента внешних сил, а также решения дифференциального уравнения движения (17). Ниже рассмотрен алгоритм и приведен документ Mathcad, в котором обеспечивается минимальное время вычислений.

4.1 Алгоритм вычислений

Угловые координаты звеньев и положение ползуна B вычисляются в явном виде по формулам (2).

Угловые скорости звеньев , отнесенных к угловой скорости кривошипа, вычисляются в явном виде по формулам (3).

Скорости центров масс звеньев отнесенных к угловой скорости кривошипа, вычисляются в явном виде по формулам (4) - (6), которые примут следующий вид

(23)

Далее, по формулам (14) и (16) вычисляется приведенный момент инерции и коэффициенты в приведенном моменте внешних сил .

Для вычисления производной от приведенного момента инерции по углу поворота ведущего звена воспользуемся явным представлением этой производной

Производные можно найти, продифференцировав по φ систему уравнений . Получим